Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view random questions on a variety of topics or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
What is the probability that two randomly selected people were born on the same day of the week? Assume that all days are equally probable.
\( \large \dfrac{1}{7}\) Hint: It doesn't matter what day the first person was born on. The probability that the second person will match is 1/7 (just designate one person the first and the other the second). Another way to look at it is that if you list the sample space of all possible pairs, e.g. (Wed, Sun), there are 49 such pairs, and 7 of them are repeats of the same day, and 7/49=1/7. | |
\( \large \dfrac{1}{14}\) Hint: What would be the sample space here? Ie, how would you list 14 things that you pick one from? | |
\( \large \dfrac{1}{42}\) Hint: If you wrote the seven days of the week on pieces of paper and put the papers in a jar, this would be the probability that the first person picked Sunday and the second picked Monday from the jar -- not the same situation. | |
\( \large \dfrac{1}{49}\) Hint: This is the probability that they are both born on a particular day, e.g. Sunday. |
Question 2 |
There are six gumballs in a bag — two red and four green. Six children take turns picking a gumball out of the bag without looking. They do not return any gumballs to the bag. What is the probability that the first two children to pick from the bag pick the red gumballs?
\( \large \dfrac{1}{3}\) Hint: This is the probability that the first child picks a red gumball, but not that the first two children pick red gumballs. | |
\( \large \dfrac{1}{8}\) Hint: Are you adding things that you should be multiplying? | |
\( \large \dfrac{1}{9}\) Hint: This would be the probability if the gumballs were returned to the bag. | |
\( \large \dfrac{1}{15}\) Hint: The probability that the first child picks red is 2/6 = 1/3. Then there are 5 gumballs in the bag, one red, so the probability that the second child picks red is 1/5. Thus 1/5 of the time, after the first child picks red, the second does too, so the probability is 1/5 x 1/3 = 1/15. |
Question 3 |
The table below gives data from various years on how many young girls drank milk.

Based on the data given above, what was the probability that a randomly chosen girl in 1990 drank milk?
\( \large \dfrac{502}{1222}\) Hint: This is the probability that a randomly chosen girl who drinks milk was in the 1989-1991 food survey. | |
\( \large \dfrac{502}{2149}\) Hint: This is the probability that a randomly chosen girl from the whole survey drank milk and was also surveyed in 1989-1991. | |
\( \large \dfrac{502}{837}\) | |
\( \large \dfrac{1222}{2149}\) Hint: This is the probability that a randomly chosen girl from any year of the survey drank milk. |
Question 4 |
The table below gives the result of a survey at a college, asking students whether they were residents or commuters:
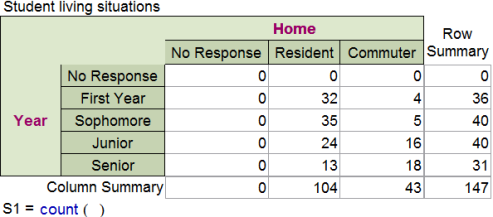
Based on the above data, what is the probability that a randomly chosen commuter student is a junior or a senior?
\( \large \dfrac{34}{43}\) | |
\( \large \dfrac{34}{71}\) Hint: This is the probability that a randomly chosen junior or senior is a commuter student. | |
\( \large \dfrac{34}{147}\) Hint: This is the probability that a randomly chosen student is a junior or senior who is a commuter. | |
\( \large \dfrac{71}{147}\) Hint: This is the probability that a randomly chosen student is a junior or a senior. |
Question 5 |
At a school fundraising event, people can buy a ticket to spin a spinner like the one below. The region that the spinner lands in tells which, if any, prize the person wins.

If 240 people buy tickets to spin the spinner, what is the best estimate of the number of keychains that will be given away?
40Hint: "Keychain" appears on the spinner twice. | |
80Hint: The probability of getting a keychain is 1/3, and so about 1/3 of the time the spinner will win. | |
100Hint: What is the probability of winning a keychain? | |
120Hint: That would be the answer for getting any prize, not a keychain specifically. |
Question 6 |
A family has four children. What is the probability that two children are girls and two are boys? Assume the the probability of having a boy (or a girl) is 50%.
\( \large \dfrac{1}{2}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{4}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{5}\) Hint: Some configurations are more probable than others -- i.e. it's more likely to have two boys and two girls than all boys. Be sure you are weighting properly. | |
\( \large \dfrac{3}{8}\) Hint: There are two possibilities for each child, so there are \(2 \times 2 \times 2 \times 2 =16\) different configurations, e.g. from oldest to youngest BBBG, BGGB, GBBB, etc. Of these configurations, there are 6 with two boys and two girls (this is the combination \(_{4}C_{2}\) or "4 choose 2"): BBGG, BGBG, BGGB, GGBB, GBGB, and GBBG. Thus the probability is 6/16=3/8. |
Question 7 |
If two fair coins are flipped, what is the probability that one will come up heads and the other tails?
\( \large \dfrac{1}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{3} \) Hint: This is a very common misconception. There are three possible outcomes -- both heads, both tails, and one of each -- but they are not equally likely. Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{2}\) Hint: The possibilities are HH, HT, TH, TT, and all are equally likely. Two of the four have one of each coin, so the probability is 2/4=1/2. | |
\( \large \dfrac{3}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. |
Question 8 |
Four children randomly line up, single file. What is the probability that they are in height order, with the shortest child in front? All of the children are different heights.
\( \large \dfrac{1}{4}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{256}
\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{16}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{24}\) Hint: The number of ways for the children to line up is \(4!=4 \times 3 \times 2 \times 1 =24\) -- there are 4 choices for who is first in line, then 3 for who is second, etc. Only one of these lines has the children in the order specified. |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.