Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view random questions on a variety of topics or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
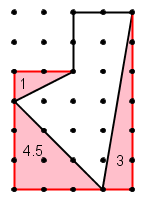
The picture below represents a board with pegs on it, where the closest distance between two pegs is 1 cm. What is the area of the pentagon shown?

Question 2 |
Each individual cube that makes up the rectangular solid depicted below has 6 inch sides. What is the surface area of the solid in square feet?

\( \large 11\text{ f}{{\text{t}}^{2}}\) Hint: Check your units and make sure you're using feet and inches consistently. | |
\( \large 16.5\text{ f}{{\text{t}}^{2}}\) Hint: Each square has surface area \(\dfrac{1}{2} \times \dfrac {1}{2}=\dfrac {1}{4}\) sq feet. There are 9 squares on the top and bottom, and 12 on each of 4 sides, for a total of 66 squares. 66 squares \(\times \dfrac {1}{4}\) sq feet/square =16.5 sq feet. | |
\( \large 66\text{ f}{{\text{t}}^{2}}\) Hint: The area of each square is not 1. | |
\( \large 2376\text{ f}{{\text{t}}^{2}}\) Hint: Read the question more carefully -- the answer is supposed to be in sq feet, not sq inches.
|
Question 3 |
What is the length of side \(\overline{BD}\) in the triangle below, where \(\angle DBA\) is a right angle?

\( \large 1\) Hint: Use the Pythagorean Theorem. | |
\( \large \sqrt{5}\) Hint: \(2^2+e^2=3^2\) or \(4+e^2=9;e^2=5; e=\sqrt{5}\). | |
\( \large \sqrt{13}\) Hint: e is not the hypotenuse. | |
\( \large 5\) Hint: Use the Pythagorean Theorem. |
Question 4 |
An above-ground swimming pool is in the shape of a regular hexagonal prism, is one meter high, and holds 65 cubic meters of water. A second pool has a base that is also a regular hexagon, but with sides twice as long as the sides in the first pool. This second pool is also one meter high. How much water will the second pool hold?
\( \large 65\text{ }{{\text{m}}^{3}}\) Hint: A bigger pool would hold more water. | |
\( \large 65\cdot 2\text{ }{{\text{m}}^{3}}\) Hint: Try a simpler example, say doubling the sides of the base of a 1 x 1 x 1 cube. | |
\( \large 65\cdot 4\text{ }{{\text{m}}^{3}}\) Hint: If we think of the pool as filled with 1 x 1 x 1 cubes (and some fractions of cubes), then scaling to the larger pool changes each 1 x 1 x 1 cube to a 2 x 2 x 1 prism, or multiplies volume by 4. | |
\( \large 65\cdot 8\text{ }{{\text{m}}^{3}}\) Hint: Try a simpler example, say doubling the sides of the base of a 1 x 1 x 1 cube. |
Question 5 |
The column below consists of two cubes and a cylinder. The cylinder has diameter y, which is also the length of the sides of each cube. The total height of the column is 5y. Which of the formulas below gives the volume of the column?

\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{4}\) Hint: The cubes each have volume \(y^3\). The cylinder has radius \(\dfrac{y}{2}\) and height \(3y\). The volume of a cylinder is \(\pi r^2 h=\pi ({\dfrac{y}{2}})^2(3y)=\dfrac{3\pi {{y}^{3}}}{4}\). Note that the volume of a cylinder is analogous to that of a prism -- area of the base times height. | |
\( \large 2{{y}^{3}}+3\pi {{y}^{3}}\) Hint: y is the diameter of the circle, not the radius. | |
\( \large {{y}^{3}}+5\pi {{y}^{3}}\) Hint: Don't forget to count both cubes. | |
\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{8}\) Hint: Make sure you know how to find the volume of a cylinder. |
Question 6 |
A car is traveling at 60 miles per hour. Which of the expressions below could be used to compute how many feet the car travels in 1 second? Note that 1 mile = 5,280 feet.
\( \large 60\dfrac{\text{miles}}{\text{hour}}\cdot 5280\dfrac{\text{feet}}{\text{mile}}\cdot 60\dfrac{\text{minutes}}{\text{hour}}\cdot 60\dfrac{\text{seconds}}{\text{minute}}
\) Hint: This answer is not in feet/second. | |
\( \large 60\dfrac{\text{miles}}{\text{hour}}\cdot 5280\dfrac{\text{feet}}{\text{mile}}\cdot \dfrac{1}{60}\dfrac{\text{hour}}{\text{minutes}}\cdot \dfrac{1}{60}\dfrac{\text{minute}}{\text{seconds}}
\) Hint: This is the only choice where the answer is in feet per second and the unit conversions are correct. | |
\( \large 60\dfrac{\text{miles}}{\text{hour}}\cdot \dfrac{1}{5280}\dfrac{\text{foot}}{\text{miles}}\cdot 60\dfrac{\text{hours}}{\text{minute}}\cdot \dfrac{1}{60}\dfrac{\text{minute}}{\text{seconds}}\) Hint: Are there really 60 hours in a minute? | |
\( \large 60\dfrac{\text{miles}}{\text{hour}}\cdot \dfrac{1}{5280}\dfrac{\text{mile}}{\text{feet}}\cdot 60\dfrac{\text{minutes}}{\text{hour}}\cdot \dfrac{1}{60}\dfrac{\text{minute}}{\text{seconds}}\) Hint: This answer is not in feet/second. |
Question 7 |
The speed of sound in dry air at 68 degrees F is 343.2 meters per second. Which of the expressions below could be used to compute the number of kilometers that a sound wave travels in 10 minutes (in dry air at 68 degrees F)?
\( \large 343.2\times 60\times 10\) Hint: In kilometers, not meters. | |
\( \large 343.2\times 60\times 10\times \dfrac{1}{1000}\) Hint: Units are meters/sec \(\times\) seconds/minute \(\times\) minutes \(\times\) kilometers/meter, and the answer is in kilometers. | |
\( \large 343.2\times \dfrac{1}{60}\times 10\) Hint: Include units and make sure answer is in kilometers. | |
\( \large 343.2\times \dfrac{1}{60}\times 10\times \dfrac{1}{1000}\) Hint: Include units and make sure answer is in kilometers. |
Question 8 |
A homeowner is planning to tile the kitchen floor with tiles that measure 6 inches by 8 inches. The kitchen floor is a rectangle that measures 10 ft by 12 ft, and there are no gaps between the tiles. How many tiles does the homeowner need?
30Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. Also, remember that 1 sq foot is 12 \(\times\) 12=144 sq inches. | |
120Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. | |
300Hint: Recheck your calculations. | |
360Hint: One way to do this is to note that 6 inches = 1/2 foot and 8 inches = 2/3 foot, so the area of each tile is 1/2 \(\times\) 2/3=1/3 sq foot, or each square foot of floor requires 3 tiles. The area of the floor is 120 square feet. Note that the tiles would fit evenly oriented in either direction, parallel to the walls. |
Question 9 |
A cylindrical soup can has diameter 7 cm and height 11 cm. The can holds g grams of soup. How many grams of the same soup could a cylindrical can with diameter 14 cm and height 33 cm hold?
\( \large 6g\) Hint: You must scale in all three dimensions. | |
\( \large 12g\) Hint: Height is multiplied by 3, and diameter and radius are multiplied by 2. Since the radius is squared, final result is multiplied by \(2^2\times 3=12\). | |
\( \large 18g\) Hint: Don't square the height scale factor. | |
\( \large 36g\) Hint: Don't square the height scale factor. |
Question 10 |
Which of the following is closest to the height of a college student in centimeters?
1.6 cmHint: This is more the height of a Lego toy college student -- less than an inch! | |
16 cmHint: Less than knee high on most college students. | |
160 cmHint: Remember, a meter stick (a little bigger than a yard stick) is 100 cm. Also good to know is that 4 inches is approximately 10 cm. | |
1600 cmHint: This college student might be taller than some campus buildings! |
Question 11 |
A family on vacation drove the first 200 miles in 4 hours and the second 200 miles in 5 hours. Which expression below gives their average speed for the entire trip?
\( \large \dfrac{200+200}{4+5}\) Hint: Average speed is total distance divided by total time. | |
\( \large \left( \dfrac{200}{4}+\dfrac{200}{5} \right)\div 2\) Hint: This seems logical, but the problem is that it weights the first 4 hours and the second 5 hours equally, when each hour should get the same weight in computing the average speed. | |
\( \large \dfrac{200}{4}+\dfrac{200}{5} \) Hint: This would be an average of 90 miles per hour! | |
\( \large \dfrac{400}{4}+\dfrac{400}{5} \) Hint: This would be an average of 180 miles per hour! Even a family of race car drivers probably doesn't have that average speed on a vacation! |
Question 12 |
The window glass below has the shape of a semi-circle on top of a square, where the side of the square has length x. It was cut from one piece of glass.
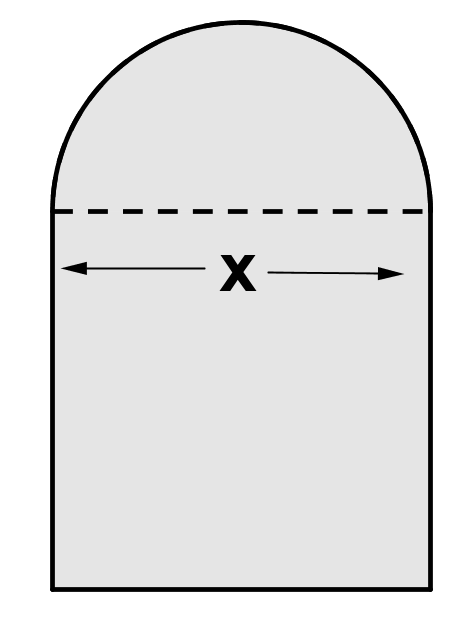
What is the perimeter of the window glass?
\( \large 3x+\dfrac{\pi x}{2}\) Hint: By definition, \(\pi\) is the ratio of the circumference of a circle to its diameter; thus the circumference is \(\pi d\). Since we have a semi-circle, its perimeter is \( \dfrac{1}{2} \pi x\). Only 3 sides of the square contribute to the perimeter. | |
\( \large 3x+2\pi x\) Hint: Make sure you know how to find the circumference of a circle. | |
\( \large 3x+\pi x\) Hint: Remember it's a semi-circle, not a circle. | |
\( \large 4x+2\pi x\) Hint: Only 3 sides of the square contribute to the perimeter. |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.