Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time. To see ten new questions, reload the page.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
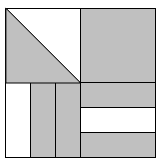
Question 1 |
\( \large \dfrac{17}{24}\) Hint: You might try adding segments so each quadrant is divided into 6 pieces with equal area -- there will be 24 regions, not all the same shape, but all the same area, with 17 of them shaded (for the top left quarter, you could also first change the diagonal line to a horizontal or vertical line that divides the square in two equal pieces and shade one) . | |
\( \large \dfrac{3}{4}\) Hint: Be sure you're taking into account the different sizes of the pieces. | |
\( \large \dfrac{2}{3}\) Hint: The bottom half of the picture is 2/3 shaded, and the top half is more than 2/3 shaded, so this answer is too small. | |
\( \large \dfrac{17}{6} \) Hint: This answer is bigger than 1, so doesn't make any sense. Be sure you are using the whole picture, not one quadrant, as the unit. |
Question 2 |
The "houses" below are made of toothpicks and gum drops.
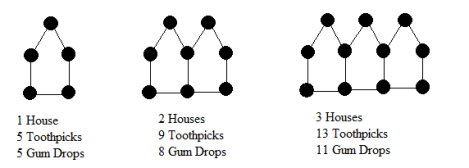
How many toothpicks are there in a row of 53 houses?
212Hint: Can the number of toothpicks be even? | |
213Hint: One way to see this is that every new "house" adds 4 toothpicks to the leftmost vertical toothpick -- so the total number is 1 plus 4 times the number of "houses." There are many other ways to look at the problem too. | |
217Hint: Try your strategy with a smaller number of "houses" so you can count and find your mistake. | |
265Hint: Remember that the "houses" overlap some walls. |
Question 3 |
Which of the following inequalities describes all values of x with \(\large \dfrac{x}{2}\le \dfrac{x}{3}\)?
\( \large x < 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \le 0\) | |
\( \large x > 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \ge 0\) Hint: Try plugging in x = 6. |
Question 4 |
Aya and Kendra want to estimate the height of a tree. On a sunny day, Aya measures Kendra's shadow as 3 meters long, and Kendra measures the tree's shadow as 15 meters long. Kendra is 1.5 meters tall. How tall is the tree?
7.5 metersHint: Here is a picture, note that the large and small right triangles are similar:  One way to do the problem is to note that there is a dilation (scale) factor of 5 on the shadows, so there must be that factor on the heights too. Another way is to note that the shadows are twice as long as the heights. | |
22.5 metersHint: Draw a picture. | |
30 metersHint: Draw a picture. | |
45 metersHint: Draw a picture. |
Question 5 |
Use the problem below to answer the question that follows:
T shirts are on sale for 20% off. Tasha paid $8.73 for a shirt. What is the regular price of the shirt? There is no tax on clothing purchases under $175.
Let p represent the regular price of these t-shirt. Which of the following equations is correct?
\( \large 0.8p=\$8.73\) Hint: 80% of the regular price = $8.73. | |
\( \large \$8.73+0.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice c. | |
\( \large 1.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice b. | |
\( \large p-0.2*\$8.73=p\) Hint: Subtract p from both sides of this equation, and you have -.2 x 8.73 =0. |
Question 6 |
The function d(x) gives the result when 12 is divided by x. Which of the following is a graph of d(x)?
 Hint: d(x) is 12 divided by x, not x divided by 12. | |
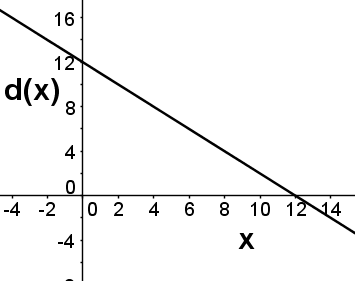 Hint: When x=2, what should d(x) be? | |
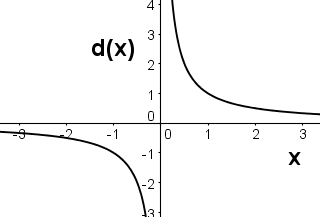 Hint: When x=2, what should d(x) be? | |
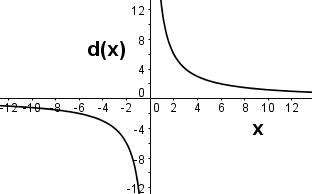 |
Question 7 |
A publisher prints a series of books with covers made of identical material and using the same thickness of paper for each page. The covers of the book together are 0.4 cm thick, and 125 pieces of the paper used together are 1 cm thick.
The publisher uses a linear function to determine the total thickness, T(n) of a book made with n sheets of paper. What are the slope and intercept of T(n)?
Intercept = 0.4 cm, Slope = 125 cm/pageHint: This would mean that each page of the book was 125 cm thick. | |
Intercept =0.4 cm, Slope = \(\dfrac{1}{125}\)cm/pageHint: The intercept is how thick the book would be with no pages in it. The slope is how much 1 extra page adds to the thickness of the book. | |
Intercept = 125 cm, Slope = 0.4 cmHint: This would mean that with no pages in the book, it would be 125 cm thick. | |
Intercept = \(\dfrac{1}{125}\)cm, Slope = 0.4 pages/cmHint: This would mean that each new page of the book made it 0.4 cm thicker. |
Question 8 |
Which of the following is equal to one million three hundred thousand?
\(\large1.3\times {{10}^{6}}\)
| |
\(\large1.3\times {{10}^{9}}\)
Hint: That's one billion three hundred million. | |
\(\large1.03\times {{10}^{6}}\)
Hint: That's one million thirty thousand. | |
\(\large1.03\times {{10}^{9}}\) Hint: That's one billion thirty million |
Question 9 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):

Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 10 |
What is the mathematical name of the three-dimensional polyhedron depicted below?

TetrahedronHint: All the faces of a tetrahedron are triangles. | |
Triangular PrismHint: A prism has two congruent, parallel bases, connected by parallelograms (since this is a right prism, the parallelograms are rectangles). | |
Triangular PyramidHint: A pyramid has one base, not two. | |
TrigonHint: A trigon is a triangle (this is not a common term). |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.