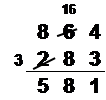Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
The letters A, and B represent digits (possibly equal) in the ten digit number x=1,438,152,A3B. For which values of A and B is x divisible by 12, but not by 9?
\( \large A = 0, B = 4\) Hint: Digits add to 31, so not divisible by 3, so not divisible by 12. | |
\( \large A = 7, B = 2\) Hint: Digits add to 36, so divisible by 9. | |
\( \large A = 0, B = 6\) Hint: Digits add to 33, divisible by 3, not 9. Last digits are 36, so divisible by 4, and hence by 12. | |
\( \large A = 4, B = 8\) Hint: Digits add to 39, divisible by 3, not 9. Last digits are 38, so not divisible by 4, so not divisible by 12. |
Question 2 |
The function d(x) gives the result when 12 is divided by x. Which of the following is a graph of d(x)?
 Hint: d(x) is 12 divided by x, not x divided by 12. | |
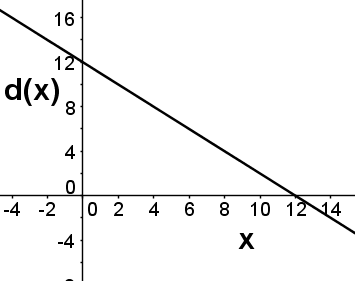 Hint: When x=2, what should d(x) be? | |
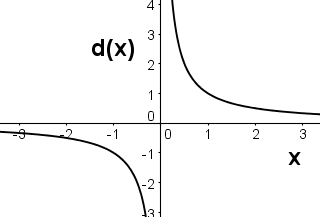 Hint: When x=2, what should d(x) be? | |
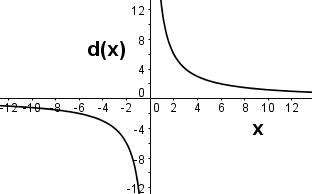 |
Question 3 |
Here is a student's work solving an equation:
\( x-4=-2x+6\)
\( x-4+4=-2x+6+4\)
\( x=-2x+10\)
\( x-2x=10\)
\( x=10\)
Which of the following statements is true?
The student‘s solution is correct.Hint: Try plugging into the original solution. | |
The student did not correctly use properties of equality.Hint: After \( x=-2x+10\), the student subtracted 2x on the left and added 2x on the right. | |
The student did not correctly use the distributive property.Hint: Distributive property is \(a(b+c)=ab+ac\). | |
The student did not correctly use the commutative property.Hint: Commutative property is \(a+b=b+a\) or \(ab=ba\). |
Question 4 |
Aya and Kendra want to estimate the height of a tree. On a sunny day, Aya measures Kendra's shadow as 3 meters long, and Kendra measures the tree's shadow as 15 meters long. Kendra is 1.5 meters tall. How tall is the tree?
7.5 metersHint: Here is a picture, note that the large and small right triangles are similar:  One way to do the problem is to note that there is a dilation (scale) factor of 5 on the shadows, so there must be that factor on the heights too. Another way is to note that the shadows are twice as long as the heights. | |
22.5 metersHint: Draw a picture. | |
30 metersHint: Draw a picture. | |
45 metersHint: Draw a picture. |
Question 5 |
A publisher prints a series of books with covers made of identical material and using the same thickness of paper for each page. The covers of the book together are 0.4 cm thick, and 125 pieces of the paper used together are 1 cm thick.
The publisher uses a linear function to determine the total thickness, T(n) of a book made with n sheets of paper. What are the slope and intercept of T(n)?
Intercept = 0.4 cm, Slope = 125 cm/pageHint: This would mean that each page of the book was 125 cm thick. | |
Intercept =0.4 cm, Slope = \(\dfrac{1}{125}\)cm/pageHint: The intercept is how thick the book would be with no pages in it. The slope is how much 1 extra page adds to the thickness of the book. | |
Intercept = 125 cm, Slope = 0.4 cmHint: This would mean that with no pages in the book, it would be 125 cm thick. | |
Intercept = \(\dfrac{1}{125}\)cm, Slope = 0.4 pages/cmHint: This would mean that each new page of the book made it 0.4 cm thicker. |
Question 6 |
There are six gumballs in a bag — two red and four green. Six children take turns picking a gumball out of the bag without looking. They do not return any gumballs to the bag. What is the probability that the first two children to pick from the bag pick the red gumballs?
\( \large \dfrac{1}{3}\) Hint: This is the probability that the first child picks a red gumball, but not that the first two children pick red gumballs. | |
\( \large \dfrac{1}{8}\) Hint: Are you adding things that you should be multiplying? | |
\( \large \dfrac{1}{9}\) Hint: This would be the probability if the gumballs were returned to the bag. | |
\( \large \dfrac{1}{15}\) Hint: The probability that the first child picks red is 2/6 = 1/3. Then there are 5 gumballs in the bag, one red, so the probability that the second child picks red is 1/5. Thus 1/5 of the time, after the first child picks red, the second does too, so the probability is 1/5 x 1/3 = 1/15. |
Question 7 |
Use the graph below to answer the question that follows.

Which of the following is a correct equation for the graph of the line depicted above?
\( \large y=-\dfrac{1}{2}x+2\) Hint: The slope is -1/2 and the y-intercept is 2. You can also try just plugging in points. For example, this is the only choice that gives y=1 when x=2. | |
\( \large 4x=2y\) Hint: This line goes through (0,0); the graph above does not. | |
\( \large y=x+2\) Hint: The line pictured has negative slope. | |
\( \large y=-x+2\) Hint: Try plugging x=4 into this equation and see if that point is on the graph above. |
Question 8 |
A family has four children. What is the probability that two children are girls and two are boys? Assume the the probability of having a boy (or a girl) is 50%.
\( \large \dfrac{1}{2}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{4}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{5}\) Hint: Some configurations are more probable than others -- i.e. it's more likely to have two boys and two girls than all boys. Be sure you are weighting properly. | |
\( \large \dfrac{3}{8}\) Hint: There are two possibilities for each child, so there are \(2 \times 2 \times 2 \times 2 =16\) different configurations, e.g. from oldest to youngest BBBG, BGGB, GBBB, etc. Of these configurations, there are 6 with two boys and two girls (this is the combination \(_{4}C_{2}\) or "4 choose 2"): BBGG, BGBG, BGGB, GGBB, GBGB, and GBBG. Thus the probability is 6/16=3/8. |
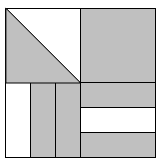
Question 9 |
\( \large \dfrac{17}{24}\) Hint: You might try adding segments so each quadrant is divided into 6 pieces with equal area -- there will be 24 regions, not all the same shape, but all the same area, with 17 of them shaded (for the top left quarter, you could also first change the diagonal line to a horizontal or vertical line that divides the square in two equal pieces and shade one) . | |
\( \large \dfrac{3}{4}\) Hint: Be sure you're taking into account the different sizes of the pieces. | |
\( \large \dfrac{2}{3}\) Hint: The bottom half of the picture is 2/3 shaded, and the top half is more than 2/3 shaded, so this answer is too small. | |
\( \large \dfrac{17}{6} \) Hint: This answer is bigger than 1, so doesn't make any sense. Be sure you are using the whole picture, not one quadrant, as the unit. |
Question 10 |
Which of the lines depicted below is a graph of \( \large y=2x-5\)?
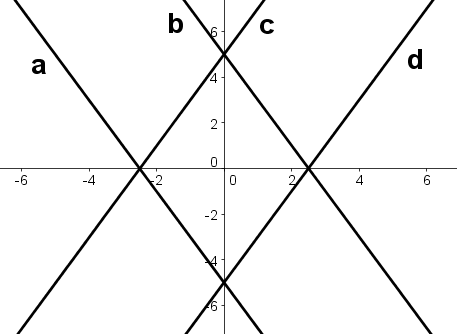
aHint: The slope of line a is negative. | |
bHint: Wrong slope and wrong intercept. | |
cHint: The intercept of line c is positive. | |
dHint: Slope is 2 -- for every increase of 1 in x, y increases by 2. Intercept is -5 -- the point (0,-5) is on the line. |
Question 11 |
Which of the numbers below is a fraction equivalent to \( 0.\bar{6}\)?
\( \large \dfrac{4}{6}\) Hint: \( 0.\bar{6}=\dfrac{2}{3}=\dfrac{4}{6}\) | |
\( \large \dfrac{3}{5}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice c, which is another way to tell that it's wrong. | |
\( \large \dfrac{6}{10}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice b, which is another way to tell that it's wrong. | |
\( \large \dfrac{1}{6}\) Hint: This is less than a half, and \( 0.\bar{6}\) is greater than a half. |
Question 12 |
Here is a number trick:
1) Pick a whole number
2) Double your number.
3) Add 20 to the above result.
4) Multiply the above by 5
5) Subtract 100
6) Divide by 10
The result is always the number that you started with! Suppose you start by picking N. Which of the equations below best demonstrates that the result after Step 6 is also N?
\( \large N*2+20*5-100\div 10=N\) Hint: Use parentheses or else order of operations is off. | |
\( \large \left( \left( 2*N+20 \right)*5-100 \right)\div 10=N\) | |
\( \large \left( N+N+20 \right)*5-100\div 10=N\) Hint: With this answer you would subtract 10, instead of subtracting 100 and then dividing by 10. | |
\( \large \left( \left( \left( N\div 10 \right)-100 \right)*5+20 \right)*2=N\) Hint: This answer is quite backwards. |
Question 13 |
The student used a method that worked for this problem and can be generalized to any subtraction problem.Hint: Note that this algorithm is taught as the "standard" algorithm in much of Europe (it's where the term "borrowing" came from -- you borrow on top and "pay back" on the bottom). | |
The student used a method that worked for this problem and that will work for any subtraction problem that only requires one regrouping; it will not work if more regrouping is required.Hint: Try some more examples. | |
The student used a method that worked for this problem and will work for all three-digit subtraction problems, but will not work for larger problems.Hint: Try some more examples. | |
The student used a method that does not work. The student made two mistakes that cancelled each other out and was lucky to get the right answer for this problem.Hint: Remember, there are many ways to do subtraction; there is no one "right" algorithm. |
Question 14 |
Use the table below to answer the question that follows:
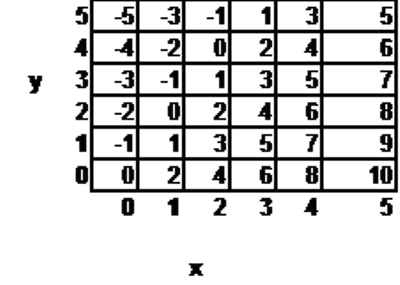
Each number in the table above represents a value W that is determined by the values of x and y. For example, when x=3 and y=1, W=5. What is the value of W when x=9 and y=14? Assume that the patterns in the table continue as shown.
\( \large W=-5\) Hint: When y is even, W is even. | |
\( \large W=4\) Hint: Note that when x increases by 1, W increases by 2, and when y increases by 1, W decreases by 1. At x=y=0, W=0, so at x=9, y=14, W has increased by \(9 \times 2\) and decreased by 14, or W=18-14=4. | |
\( \large W=6\) Hint: Try fixing x or y at 0, and start by finding W for x=0 y=14 or x=9, y=0. | |
\( \large W=32\) Hint: Try fixing x or y at 0, and start by finding W for x=0 y=14 or x=9, y=0. |
Question 15 |
Use the graph below to answer the question that follows.

If the polygon shown above is reflected about the y axis and then rotated 90 degrees clockwise about the origin, which of the following graphs is the result?
 Hint: Try following the point (1,4) to see where it goes after each transformation. | |
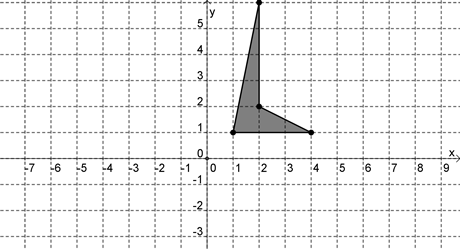 | |

Hint: Make sure you're reflecting in the correct axis. | |
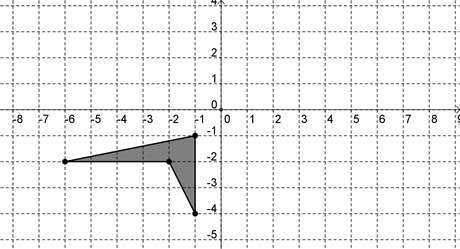 Hint: Make sure you're rotating the correct direction. |
Question 16 |
The column below consists of two cubes and a cylinder. The cylinder has diameter y, which is also the length of the sides of each cube. The total height of the column is 5y. Which of the formulas below gives the volume of the column?

\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{4}\) Hint: The cubes each have volume \(y^3\). The cylinder has radius \(\dfrac{y}{2}\) and height \(3y\). The volume of a cylinder is \(\pi r^2 h=\pi ({\dfrac{y}{2}})^2(3y)=\dfrac{3\pi {{y}^{3}}}{4}\). Note that the volume of a cylinder is analogous to that of a prism -- area of the base times height. | |
\( \large 2{{y}^{3}}+3\pi {{y}^{3}}\) Hint: y is the diameter of the circle, not the radius. | |
\( \large {{y}^{3}}+5\pi {{y}^{3}}\) Hint: Don't forget to count both cubes. | |
\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{8}\) Hint: Make sure you know how to find the volume of a cylinder. |
Question 17 |
Which of the following nets will not fold into a cube?
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
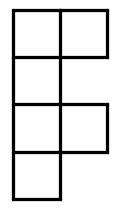 | |
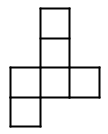 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). |
Question 18 |
Use the samples of a student's work below to answer the question that follows:
\( \large \dfrac{2}{3}\times \dfrac{3}{4}=\dfrac{4\times 2}{3\times 3}=\dfrac{8}{9}\) \( \large \dfrac{2}{5}\times \dfrac{7}{7}=\dfrac{7\times 2}{5\times 7}=\dfrac{2}{5}\) \( \large \dfrac{7}{6}\times \dfrac{3}{4}=\dfrac{4\times 7}{6\times 3}=\dfrac{28}{18}=\dfrac{14}{9}\)Which of the following best describes the mathematical validity of the algorithm the student is using?
It is not valid. It never produces the correct answer.Hint: In the middle example,the answer is correct. | |
It is not valid. It produces the correct answer in a few special cases, but it‘s still not a valid algorithm.Hint: Note that this algorithm gives a/b divided by c/d, not a/b x c/d, but some students confuse multiplication and cross-multiplication. If a=0 or if c/d =1, division and multiplication give the same answer. | |
It is valid if the rational numbers in the multiplication problem are in lowest terms.Hint: Lowest terms is irrelevant. | |
It is valid for all rational numbers.Hint: Can't be correct as the first and last examples have the wrong answers. |
Question 19 |
A teacher has a list of all the countries in the world and their populations in March 2012. She is going to have her students use technology to compute the mean and median of the numbers on the list. Which of the following statements is true?
The teacher can be sure that the mean and median will be the same without doing any computation.Hint: Does this make sense? How likely is it that the mean and median of any large data set will be the same? | |
The teacher can be sure that the mean is bigger than the median without doing any computation.Hint: This is a skewed distribution, and very large countries like China and India contribute huge numbers to the mean, but are counted the same as small countries like Luxembourg in the median (the same thing happens w/data on salaries, where a few very high income people tilt the mean -- that's why such data is usually reported as medians). | |
The teacher can be sure that the median is bigger than the mean without doing any computation.Hint: Think about a set of numbers like 1, 2, 3, 4, 10,000 -- how do the mean/median compare? How might that relate to countries of the world? | |
There is no way for the teacher to know the relative size of the mean and median without computing them.Hint: Knowing the shape of the distribution of populations does give us enough info to know the relative size of the mean and median, even without computing them. |
Question 20 |
Which of the lists below contains only irrational numbers?
\( \large\pi , \quad \sqrt{6},\quad \sqrt{\dfrac{1}{2}}\) | |
\( \large\pi , \quad \sqrt{9}, \quad \pi +1\) Hint: \( \sqrt{9}=3\) | |
\( \large\dfrac{1}{3},\quad \dfrac{5}{4},\quad \dfrac{2}{9}\) Hint: These are all rational. | |
\( \large-3,\quad 14,\quad 0\) Hint: These are all rational. |
Question 21 |
The equation \( \large F=\frac{9}{5}C+32\) is used to convert a temperature measured in Celsius to the equivalent Farentheit temperature.
A patient's temperature increased by 1.5° Celcius. By how many degrees Fahrenheit did her temperature increase?
1.5°Hint: Celsius and Fahrenheit don't increase at the same rate. | |
1.8°Hint: That's how much the Fahrenheit temp increases when the Celsius temp goes up by 1 degree. | |
2.7°Hint: Each degree increase in Celsius corresponds to a \(\dfrac{9}{5}=1.8\) degree increase in Fahrenheit. Thus the increase is 1.8+0.9=2.7. | |
Not enough information.Hint: A linear equation has constant slope, which means that every increase of the same amount in one variable, gives a constant increase in the other variable. It doesn't matter what temperature the patient started out at. |
Question 22 |
A class is using base-ten block to represent numbers. A large cube represents 1000, a flat represents 100, a rod represents 10, and a little cube represents 1. Which of these is not a correct representation for 2,347?
23 flats, 4 rods, 7 little cubesHint: Be sure you read the question carefully: 2300+40+7=2347 | |
2 large cubes, 3 flats, 47 rodsHint: 2000+300+470 \( \neq\) 2347 | |
2 large cubes, 34 rods, 7 little cubesHint: Be sure you read the question carefully: 2000+340+7=2347 | |
2 large cubes, 3 flats, 4 rods, 7 little cubesHint: Be sure you read the question carefully: 2000+300+40+7=2347 |
Question 23 |
Which of the following is the equation of a linear function?
\( \large y={{x}^{2}}+2x+7\) Hint: This is a quadratic function. | |
\( \large y={{2}^{x}}\) Hint: This is an exponential function. | |
\( \large y=\dfrac{15}{x}\) Hint: This is an inverse function. | |
\( \large y=x+(x+4)\) Hint: This is a linear function, y=2x+4, it's graph is a straight line with slope 2 and y-intercept 4. |
Question 24 |
Taxicab fares in Boston (Spring 2012) are $2.60 for the first \(\dfrac{1}{7}\) of a mile or less and $0.40 for each \(\dfrac{1}{7}\) of a mile after that.
Let d represent the distance a passenger travels in miles (with \(d>\dfrac{1}{7}\)). Which of the following expressions represents the total fare?
\( \large \$2.60+\$0.40d\) Hint: It's 40 cents for 1/7 of a mile, not per mile. | |
\( \large \$2.60+\$0.40\dfrac{d}{7}\) Hint: According to this equation, going 7 miles would cost $3; does that make sense? | |
\( \large \$2.20+\$2.80d\) Hint: You can think of the fare as $2.20 to enter the cab, and then $0.40 for each 1/7 of a mile, including the first 1/7 of a mile (or $2.80 per mile).
Alternatively, you pay $2.60 for the first 1/7 of a mile, and then $2.80 per mile for d-1/7 miles. The total is 2.60+2.80(d-1/7) = 2.60+ 2.80d -.40 = 2.20+2.80d. | |
\( \large \$2.60+\$2.80d\) Hint: Don't count the first 1/7 of a mile twice. |
Question 25 |
Which of the following is an irrational number?
\( \large \sqrt[3]{8}\) Hint: This answer is the cube root of 8. Since 2 x 2 x 2 =8, this is equal to 2, which is rational because 2 = 2/1. | |
\( \large \sqrt{8}\) Hint: It is not trivial to prove that this is irrational, but you can get this answer by eliminating the other choices. | |
\( \large \dfrac{1}{8}\) Hint: 1/8 is the RATIO of two integers, so it is rational. | |
\( \large -8\) Hint: Negative integers are also rational, -8 = -8/1, a ratio of integers. |
Question 26 |
The expression \( \large{{8}^{3}}\cdot {{2}^{-10}}\) is equal to which of the following?
\( \large 2\) Hint: Write \(8^3\) as a power of 2. | |
\( \large \dfrac{1}{2}\) Hint: \(8^3 \cdot {2}^{-10}={(2^3)}^3 \cdot {2}^{-10}\) =\(2^9 \cdot {2}^{-10} =2^{-1}\) | |
\( \large 16\) Hint: Write \(8^3\) as a power of 2. | |
\( \large \dfrac{1}{16}\) Hint: Write \(8^3\) as a power of 2. |
Question 27 |
Below are front, side, and top views of a three-dimensional solid.
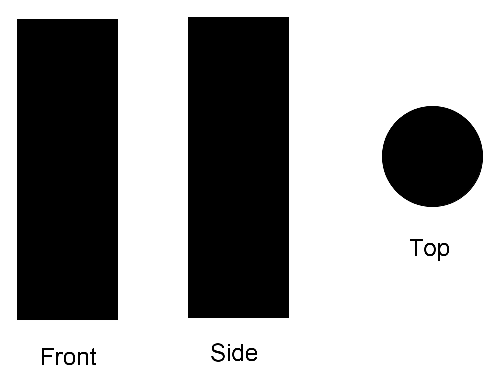
Which of the following could be the solid shown above?
A sphereHint: All views would be circles. | |
A cylinder | |
A coneHint: Two views would be triangles, not rectangles. | |
A pyramidHint: How would one view be a circle? |
Question 28 |
The histogram below shows the frequency of a class's scores on a 4 question quiz.
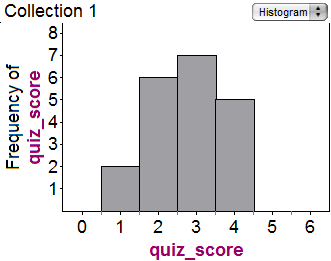
What was the mean score on the quiz?
\( \large 2.75\) Hint: There were 20 students who took the quiz. Total points earned: \(2 \times 1+6 \times 2+ 7\times 3+5 \times 4=55\), and 55/20 = 2.75. | |
\( \large 2\) Hint: How many students are there total? Did you count them all? | |
\( \large 3\) Hint: How many students are there total? Did you count them all? Be sure you're finding the mean, not the median or the mode. | |
\( \large 2.5\) Hint: How many students are there total? Did you count them all? Don't just take the mean of 1, 2, 3, 4 -- you have to weight them properly. |
Question 29 |
P is a prime number that divides 240. Which of the following must be true?
P divides 30Hint: 2, 3, and 5 are the prime factors of 240, and all divide 30. | |
P divides 48Hint: P=5 doesn't work. | |
P divides 75Hint: P=2 doesn't work. | |
P divides 80Hint: P=3 doesn't work. |
Question 30 |
Which of the following is equivalent to
\( \large A-B+C\div D\times E\)?
\( \large A-B-\dfrac{C}{DE}
\) Hint: In the order of operations, multiplication and division have the same priority, so do them left to right; same with addition and subtraction. | |
\( \large A-B+\dfrac{CE}{D}\) Hint: In practice, you're better off using parentheses than writing an expression like the one in the question. The PEMDAS acronym that many people memorize is misleading. Multiplication and division have equal priority and are done left to right. They have higher priority than addition and subtraction. Addition and subtraction also have equal priority and are done left to right. | |
\( \large \dfrac{AE-BE+CE}{D}\) Hint: Use order of operations, don't just compute left to right. | |
\( \large A-B+\dfrac{C}{DE}\) Hint: In the order of operations, multiplication and division have the same priority, so do them left to right |
Question 31 |
What is the length of side \(\overline{BD}\) in the triangle below, where \(\angle DBA\) is a right angle?

\( \large 1\) Hint: Use the Pythagorean Theorem. | |
\( \large \sqrt{5}\) Hint: \(2^2+e^2=3^2\) or \(4+e^2=9;e^2=5; e=\sqrt{5}\). | |
\( \large \sqrt{13}\) Hint: e is not the hypotenuse. | |
\( \large 5\) Hint: Use the Pythagorean Theorem. |
Question 32 |
Which of the numbers below is not equivalent to 4%?
\( \large \dfrac{1}{25}\) Hint: 1/25=4/100, so this is equal to 4% (be sure you read the question correctly). | |
\( \large \dfrac{4}{100}\) Hint: 4/100=4% (be sure you read the question correctly). | |
\( \large 0.4\) Hint: 0.4=40% so this is not equal to 4% | |
\( \large 0.04\) Hint: 0.04=4/100, so this is equal to 4% (be sure you read the question correctly). |
Question 33 |
Solve for x: \(\large 4-\dfrac{2}{3}x=2x\)
\( \large x=3\) Hint: Try plugging x=3 into the equation. | |
\( \large x=-3\) Hint: Left side is positive, right side is negative when you plug this in for x. | |
\( \large x=\dfrac{3}{2}\) Hint: One way to solve: \(4=\dfrac{2}{3}x+2x\) \(=\dfrac{8}{3}x\).\(x=\dfrac{3 \times 4}{8}=\dfrac{3}{2}\). Another way is to just plug x=3/2 into the equation and see that each side equals 3 -- on a multiple choice test, you almost never have to actually solve for x. | |
\( \large x=-\dfrac{3}{2}\) Hint: Left side is positive, right side is negative when you plug this in for x. |
Question 34 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):

Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 35 |
Kendra is trying to decide which fraction is greater, \( \dfrac{4}{7}\) or \( \dfrac{5}{8}\). Which of the following answers shows the best reasoning?
\( \dfrac{4}{7}\) is \( \dfrac{3}{7}\)away from 1, and \( \dfrac{5}{8}\) is \( \dfrac{3}{8}\)away from 1. Since eighth‘s are smaller than seventh‘s, \( \dfrac{5}{8}\) is closer to 1, and is the greater of the two fractions. | |
\( 7-4=3\) and \( 8-5=3\), so the fractions are equal.Hint: Not how to compare fractions. By this logic, 1/2 and 3/4 are equal, but 1/2 and 2/4 are not. | |
\( 4\times 8=32\) and \( 7\times 5=35\). Since \( 32<35\) , \( \dfrac{5}{8}<\dfrac{4}{7}\)Hint: Starts out as something that works, but the conclusion is wrong. 4/7 = 32/56 and 5/8 = 35/56. The cross multiplication gives the numerators, and 35/56 is bigger. | |
\( 4<5\) and \( 7<8\), so \( \dfrac{4}{7}<\dfrac{5}{8}\)Hint: Conclusion is correct, logic is wrong. With this reasoning, 1/2 would be less than 2/100,000. |
Question 36 |
The chairs in a large room can be arranged in rows of 18, 25, or 60 with no chairs left over. If C is the smallest possible number of chairs in the room, which of the following inequalities does C satisfy?
\( \large C\le 300\) Hint: Find the LCM. | |
\( \large 300 < C \le 500 \) Hint: Find the LCM. | |
\( \large 500 < C \le 700 \) Hint: Find the LCM. | |
\( \large C>700\) Hint: The LCM is 900, which is the smallest number of chairs. |
Question 37 |
A biology class requires a lab fee, which is a whole number of dollars, and the same amount for all students. On Monday the instructor collected $70 in fees, on Tuesday she collected $126, and on Wednesday she collected $266. What is the largest possible amount the fee could be?
$2Hint: A possible fee, but not the largest possible fee. Check the other choices to see which are factors of all three numbers. | |
$7Hint: A possible fee, but not the largest possible fee. Check the other choices to see which are factors of all three numbers. | |
$14Hint: This is the greatest common factor of 70, 126, and 266. | |
$70Hint: Not a factor of 126 or 266, so couldn't be correct. |
Question 38 |
The table below gives data from various years on how many young girls drank milk.

Based on the data given above, what was the probability that a randomly chosen girl in 1990 drank milk?
\( \large \dfrac{502}{1222}\) Hint: This is the probability that a randomly chosen girl who drinks milk was in the 1989-1991 food survey. | |
\( \large \dfrac{502}{2149}\) Hint: This is the probability that a randomly chosen girl from the whole survey drank milk and was also surveyed in 1989-1991. | |
\( \large \dfrac{502}{837}\) | |
\( \large \dfrac{1222}{2149}\) Hint: This is the probability that a randomly chosen girl from any year of the survey drank milk. |
Question 39 |
If x is an integer, which of the following must also be an integer?
\( \large \dfrac{x}{2}\) Hint: If x is odd, then \( \dfrac{x}{2} \) is not an integer, e.g. 3/2 = 1.5. | |
\( \large \dfrac{2}{x}\) Hint: Only an integer if x = -2, -1, 1, or 2. | |
\( \large-x\) Hint: -1 times any integer is still an integer. | |
\(\large\sqrt{x}\) Hint: Usually not an integer, e.g. \( \sqrt{2} \approx 1.414 \). |
Question 40 |
The table below gives the result of a survey at a college, asking students whether they were residents or commuters:
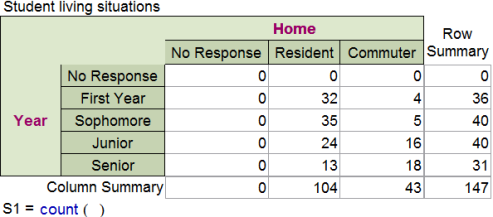
Based on the above data, what is the probability that a randomly chosen commuter student is a junior or a senior?
\( \large \dfrac{34}{43}\) | |
\( \large \dfrac{34}{71}\) Hint: This is the probability that a randomly chosen junior or senior is a commuter student. | |
\( \large \dfrac{34}{147}\) Hint: This is the probability that a randomly chosen student is a junior or senior who is a commuter. | |
\( \large \dfrac{71}{147}\) Hint: This is the probability that a randomly chosen student is a junior or a senior. |
Question 41 |
Which of the lists below is in order from least to greatest value?
\( \large \dfrac{1}{2},\quad \dfrac{1}{3},\quad \dfrac{1}{4},\quad \dfrac{1}{5}\) Hint: This is ordered from greatest to least. | |
\( \large \dfrac{1}{3},\quad \dfrac{2}{7},\quad \dfrac{3}{8},\quad \dfrac{4}{11}\) Hint: 1/3 = 2/6 is bigger than 2/7. | |
\( \large \dfrac{1}{4},\quad \dfrac{2}{5},\quad \dfrac{2}{3},\quad \dfrac{4}{5}\) Hint: One way to look at this: 1/4 and 2/5 are both less than 1/2, and 2/3 and 4/5 are both greater than 1/2. 1/4 is 25% and 2/5 is 40%, so 2/5 is greater. The distance from 2/3 to 1 is 1/3 and from 4/5 to 1 is 1/5, and 1/5 is less than 1/3, so 4/5 is bigger. | |
\( \large \dfrac{7}{8},\quad \dfrac{6}{7},\quad \dfrac{5}{6},\quad \dfrac{4}{5}\) Hint: This is in order from greatest to least. |
Question 42 |
How many factors does 80 have?
\( \large8\) Hint: Don't forget 1 and 80. | |
\( \large9\) Hint: Only perfect squares have an odd number of factors -- otherwise factors come in pairs. | |
\( \large10\) Hint: 1,2,4,5,8,10,16,20,40,80 | |
\( \large12\) Hint: Did you count a number twice? Include a number that isn't a factor? |
Question 43 |
The Venn Diagram below gives data on the number of seniors, athletes, and vegetarians in the student body at a college:
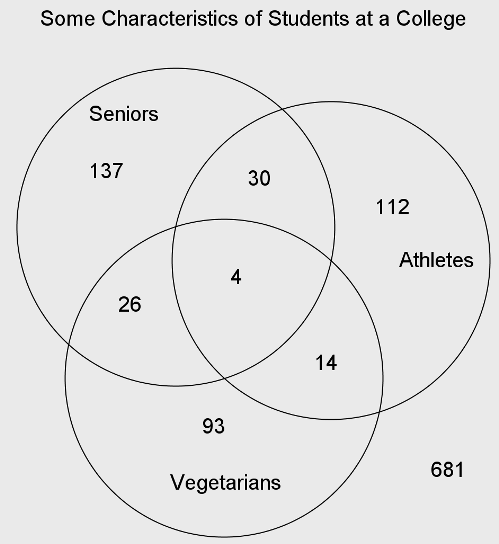
How many students at the college are seniors who are not vegetarians?
\( \large 137\) Hint: Doesn't include the senior athletes who are not vegetarians. | |
\( \large 167\) | |
\( \large 197\) Hint: That's all seniors, including vegetarians. | |
\( \large 279\) Hint: Includes all athletes who are not vegetarians, some of whom are not seniors. |
Question 44 |
Use the expression below to answer the question that follows.
\(\large \dfrac{\left( 155 \right)\times \left( 6,124 \right)}{977}\)
Which of the following is the best estimate of the expression above?
100Hint: 6124/977 is approximately 6. | |
200Hint: 6124/977 is approximately 6. | |
1,000Hint: 6124/977 is approximately 6. 155 is approximately 150, and \( 6 \times 150 = 3 \times 300 = 900\), so this answer is closest. | |
2,000Hint: 6124/977 is approximately 6. |
Question 45 |
What is the probability that two randomly selected people were born on the same day of the week? Assume that all days are equally probable.
\( \large \dfrac{1}{7}\) Hint: It doesn't matter what day the first person was born on. The probability that the second person will match is 1/7 (just designate one person the first and the other the second). Another way to look at it is that if you list the sample space of all possible pairs, e.g. (Wed, Sun), there are 49 such pairs, and 7 of them are repeats of the same day, and 7/49=1/7. | |
\( \large \dfrac{1}{14}\) Hint: What would be the sample space here? Ie, how would you list 14 things that you pick one from? | |
\( \large \dfrac{1}{42}\) Hint: If you wrote the seven days of the week on pieces of paper and put the papers in a jar, this would be the probability that the first person picked Sunday and the second picked Monday from the jar -- not the same situation. | |
\( \large \dfrac{1}{49}\) Hint: This is the probability that they are both born on a particular day, e.g. Sunday. |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.