Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view random questions on a variety of topics or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
Which of the lists below is in order from least to greatest value?
\( \large \dfrac{1}{2},\quad \dfrac{1}{3},\quad \dfrac{1}{4},\quad \dfrac{1}{5}\) Hint: This is ordered from greatest to least. | |
\( \large \dfrac{1}{3},\quad \dfrac{2}{7},\quad \dfrac{3}{8},\quad \dfrac{4}{11}\) Hint: 1/3 = 2/6 is bigger than 2/7. | |
\( \large \dfrac{1}{4},\quad \dfrac{2}{5},\quad \dfrac{2}{3},\quad \dfrac{4}{5}\) Hint: One way to look at this: 1/4 and 2/5 are both less than 1/2, and 2/3 and 4/5 are both greater than 1/2. 1/4 is 25% and 2/5 is 40%, so 2/5 is greater. The distance from 2/3 to 1 is 1/3 and from 4/5 to 1 is 1/5, and 1/5 is less than 1/3, so 4/5 is bigger. | |
\( \large \dfrac{7}{8},\quad \dfrac{6}{7},\quad \dfrac{5}{6},\quad \dfrac{4}{5}\) Hint: This is in order from greatest to least. |
Question 2 |
Which of the lists below is in order from least to greatest value?
\( \large -0.044,\quad -0.04,\quad 0.04,\quad 0.044\) Hint: These are easier to compare if you add trailing zeroes (this is finding a common denominator) -- all in thousandths, -0.044, -0.040,0 .040, 0.044. The middle two numbers, -0.040 and 0.040 can be modeled as owing 4 cents and having 4 cents. The outer two numbers are owing or having a bit more. | |
\( \large -0.04,\quad -0.044,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. | |
\( \large -0.04,\quad -0.044,\quad 0.04,\quad 0.044\) Hint: -0.04=-0.040, which is greater than \(-0.044\). | |
\( \large -0.044,\quad -0.04,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. |
Question 3 |
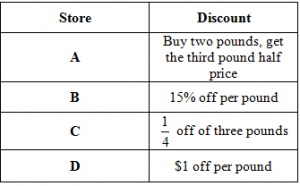
Use the table below to answer the question that follows:
Gordon wants to buy three pounds of nuts. Each of the stores above ordinarily sells the nuts for $4.99 a pound, but is offering a discount this week. At which store can he buy the nuts for the least amount of money?
Store AHint: This would save about $2.50. You can quickly see that D saves more. | |
Store BHint: This saves 15% and C saves 25%. | |
Store C | |
Store DHint: This is about 20% off, which is less of a discount than C. |
Question 4 |
Which of the numbers below is the decimal equivalent of \( \dfrac{3}{8}?\)
0.38Hint: If you are just writing the numerator next to the denominator then your technique is way off, but by coincidence your answer is close; try with 2/3 and 0.23 is nowhere near correct. | |
0.125Hint: This is 1/8, not 3/8. | |
0.375 | |
0.83Hint: 3/8 is less than a half, and 0.83 is more than a half, so they can't be equal. |
Question 5 |
Which of the numbers below is a fraction equivalent to \( 0.\bar{6}\)?
\( \large \dfrac{4}{6}\) Hint: \( 0.\bar{6}=\dfrac{2}{3}=\dfrac{4}{6}\) | |
\( \large \dfrac{3}{5}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice c, which is another way to tell that it's wrong. | |
\( \large \dfrac{6}{10}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice b, which is another way to tell that it's wrong. | |
\( \large \dfrac{1}{6}\) Hint: This is less than a half, and \( 0.\bar{6}\) is greater than a half. |
Question 6 |
Which of the numbers below is not equivalent to 4%?
\( \large \dfrac{1}{25}\) Hint: 1/25=4/100, so this is equal to 4% (be sure you read the question correctly). | |
\( \large \dfrac{4}{100}\) Hint: 4/100=4% (be sure you read the question correctly). | |
\( \large 0.4\) Hint: 0.4=40% so this is not equal to 4% | |
\( \large 0.04\) Hint: 0.04=4/100, so this is equal to 4% (be sure you read the question correctly). |
Question 7 |
Given that 10 cm is approximately equal to 4 inches, which of the following expressions models a way to find out approximately how many inches are equivalent to 350 cm?
\( \large 350\times \left( \dfrac{10}{4} \right)\) Hint: The final result should be smaller than 350, and this answer is bigger. | |
\( \large 350\times \left( \dfrac{4}{10} \right)\) Hint: Dimensional analysis can help here: \(350 \text{cm} \times \dfrac{4 \text{in}}{10 \text{cm}}\). The cm's cancel and the answer is in inches. | |
\( \large (10-4) \times 350
\) Hint: This answer doesn't make much sense. Try with a simpler example (e.g. 20 cm not 350 cm) to make sure that your logic makes sense. | |
\( \large (350-10) \times 4\) Hint: This answer doesn't make much sense. Try with a simpler example (e.g. 20 cm not 350 cm) to make sure that your logic makes sense. |
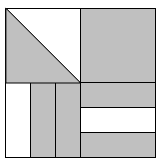
Question 8 |
\( \large \dfrac{17}{24}\) Hint: You might try adding segments so each quadrant is divided into 6 pieces with equal area -- there will be 24 regions, not all the same shape, but all the same area, with 17 of them shaded (for the top left quarter, you could also first change the diagonal line to a horizontal or vertical line that divides the square in two equal pieces and shade one) . | |
\( \large \dfrac{3}{4}\) Hint: Be sure you're taking into account the different sizes of the pieces. | |
\( \large \dfrac{2}{3}\) Hint: The bottom half of the picture is 2/3 shaded, and the top half is more than 2/3 shaded, so this answer is too small. | |
\( \large \dfrac{17}{6} \) Hint: This answer is bigger than 1, so doesn't make any sense. Be sure you are using the whole picture, not one quadrant, as the unit. |
Question 9 |
The picture below shows identical circles drawn on a piece of paper. The rectangle represents an index card that is blocking your view of \( \dfrac{3}{5}\) of the circles on the paper. How many circles are covered by the rectangle?

4Hint: The card blocks more than half of the circles, so this number is too small. | |
5Hint: The card blocks more than half of the circles, so this number is too small. | |
8Hint: The card blocks more than half of the circles, so this number is too small. | |
12Hint: 2/5 of the circles or 8 circles are showing. Thus 4 circles represent 1/5 of the circles, and \(4 \times 5=20\) circles represent 5/5 or all the circles. Thus 12 circles are hidden. |
Question 10 |
| I. \(\large \dfrac{1}{2}+\dfrac{1}{3}\) | II. \( \large .400000\) | III. \(\large\dfrac{1}{5}+\dfrac{1}{5}\) |
| IV. \( \large 40\% \) | V. \( \large 0.25 \) | VI. \(\large\dfrac{14}{35}\) |
Which of the lists below includes all of the above expressions that are equivalent to \( \dfrac{2}{5}\)?
I, III, V, VIHint: I and V are not at all how fractions and decimals work. | |
III, VIHint: These are right, but there are more. | |
II, III, VIHint: These are right, but there are more. | |
II, III, IV, VI |
Question 11 |
Below is a portion of a number line.

Point A is one-quarter of the distance from 0.26 to 0.28. What number is represented by point A?
\( \large0.26\) Hint: Please reread the question. | |
\( \large0.2625\) Hint: This is one-quarter of the distance between 0.26 and 0.27, which is not what the question asked. | |
\( \large0.265\) | |
\( \large0.27\) Hint: Please read the question more carefully. This answer would be correct if Point A were halfway between the tick marks, but it's not. |
Question 12 |
Below is a portion of a number line:

Point B is halfway between two tick marks. What number is represented by Point B?
\( \large 0.645\) Hint: That point is marked on the line, to the right. | |
\( \large 0.6421\) Hint: That point is to the left of point B. | |
\( \large 0.6422\) Hint: That point is to the left of point B. | |
\( \large 0.6425\) |
Question 13 |
Kendra is trying to decide which fraction is greater, \( \dfrac{4}{7}\) or \( \dfrac{5}{8}\). Which of the following answers shows the best reasoning?
\( \dfrac{4}{7}\) is \( \dfrac{3}{7}\)away from 1, and \( \dfrac{5}{8}\) is \( \dfrac{3}{8}\)away from 1. Since eighth‘s are smaller than seventh‘s, \( \dfrac{5}{8}\) is closer to 1, and is the greater of the two fractions. | |
\( 7-4=3\) and \( 8-5=3\), so the fractions are equal.Hint: Not how to compare fractions. By this logic, 1/2 and 3/4 are equal, but 1/2 and 2/4 are not. | |
\( 4\times 8=32\) and \( 7\times 5=35\). Since \( 32<35\) , \( \dfrac{5}{8}<\dfrac{4}{7}\)Hint: Starts out as something that works, but the conclusion is wrong. 4/7 = 32/56 and 5/8 = 35/56. The cross multiplication gives the numerators, and 35/56 is bigger. | |
\( 4<5\) and \( 7<8\), so \( \dfrac{4}{7}<\dfrac{5}{8}\)Hint: Conclusion is correct, logic is wrong. With this reasoning, 1/2 would be less than 2/100,000. |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.