Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time. To see ten new questions, reload the page.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
If x is an integer, which of the following must also be an integer?
\( \large \dfrac{x}{2}\) Hint: If x is odd, then \( \dfrac{x}{2} \) is not an integer, e.g. 3/2 = 1.5. | |
\( \large \dfrac{2}{x}\) Hint: Only an integer if x = -2, -1, 1, or 2. | |
\( \large-x\) Hint: -1 times any integer is still an integer. | |
\(\large\sqrt{x}\) Hint: Usually not an integer, e.g. \( \sqrt{2} \approx 1.414 \). |
Question 2 |
P is a prime number that divides 240. Which of the following must be true?
P divides 30Hint: 2, 3, and 5 are the prime factors of 240, and all divide 30. | |
P divides 48Hint: P=5 doesn't work. | |
P divides 75Hint: P=2 doesn't work. | |
P divides 80Hint: P=3 doesn't work. |
Question 3 |
In the triangle below, \(\overline{AC}\cong \overline{AD}\cong \overline{DE}\) and \(m\angle CAD=100{}^\circ \). What is \(m\angle DAE\)?
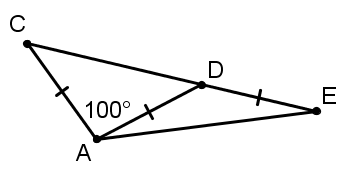
\( \large 20{}^\circ \) Hint: Angles ACD and ADC are congruent since they are base angles of an isosceles triangle. Since the angles of a triangle sum to 180, they sum to 80, and they are 40 deg each. Thus angle ADE is 140 deg, since it makes a straight line with angle ADC. Angles DAE and DEA are base angles of an isosceles triangle and thus congruent-- they sum to 40 deg, so are 20 deg each. | |
\( \large 25{}^\circ \) Hint: If two sides of a triangle are congruent, then it's isosceles, and the base angles of an isosceles triangle are equal. | |
\( \large 30{}^\circ \) Hint: If two sides of a triangle are congruent, then it's isosceles, and the base angles of an isosceles triangle are equal. | |
\( \large 40{}^\circ \) Hint: Make sure you're calculating the correct angle. |
Question 4 |
Which of the following nets will not fold into a cube?
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
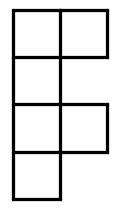 | |
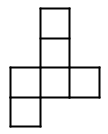 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). |
Question 5 |
The polygon depicted below is drawn on dot paper, with the dots spaced 1 unit apart. What is the perimeter of the polygon?

\( \large 18+\sqrt{2} \text{ units}\) Hint: Be careful with the Pythagorean Theorem. | |
\( \large 18+2\sqrt{2}\text{ units}\) Hint: There are 13 horizontal or vertical 1 unit segments. The longer diagonal is the hypotenuse of a 3-4-5 right triangle, so its length is 5 units. The shorter diagonal is the hypotenuse of a 45-45-90 right triangle with side 2, so its hypotenuse has length \(2 \sqrt{2}\). | |
\( \large 18 \text{ units}
\) Hint: Use the Pythagorean Theorem to find the lengths of the diagonal segments. | |
\( \large 20 \text{ units}\) Hint: Use the Pythagorean Theorem to find the lengths of the diagonal segments. |
Question 6 |
The "houses" below are made of toothpicks and gum drops.
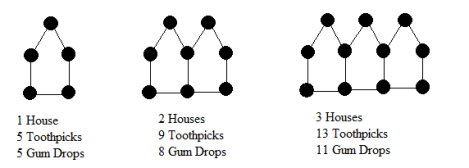
Which of the following does not represent the number of gumdrops in a row of h houses?
\( \large 2+3h\) Hint: Think of this as start with 2 gumdrops on the left wall, and then add 3 gumdrops for each house. | |
\( \large 5+3(h-1)\) Hint: Think of this as start with one house, and then add 3 gumdrops for each of the other h-1 houses. | |
\( \large h+(h+1)+(h+1)\) Hint: Look at the gumdrops in 3 rows: h gumdrops for the "rooftops," h+1 for the tops of the vertical walls, and h+1 for the floors. | |
\( \large 5+3h\) Hint: This one is not a correct equation (which makes it the correct answer!). Compare to choice A. One of them has to be wrong, as they differ by 3. |
Question 7 |
The column below consists of two cubes and a cylinder. The cylinder has diameter y, which is also the length of the sides of each cube. The total height of the column is 5y. Which of the formulas below gives the volume of the column?

\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{4}\) Hint: The cubes each have volume \(y^3\). The cylinder has radius \(\dfrac{y}{2}\) and height \(3y\). The volume of a cylinder is \(\pi r^2 h=\pi ({\dfrac{y}{2}})^2(3y)=\dfrac{3\pi {{y}^{3}}}{4}\). Note that the volume of a cylinder is analogous to that of a prism -- area of the base times height. | |
\( \large 2{{y}^{3}}+3\pi {{y}^{3}}\) Hint: y is the diameter of the circle, not the radius. | |
\( \large {{y}^{3}}+5\pi {{y}^{3}}\) Hint: Don't forget to count both cubes. | |
\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{8}\) Hint: Make sure you know how to find the volume of a cylinder. |
Question 8 |
In each expression below N represents a negative integer. Which expression could have a negative value?
\( \large {{N}^{2}}\) Hint: Squaring always gives a non-negative value. | |
\( \large 6-N\) Hint: A story problem for this expression is, if it was 6 degrees out at noon and N degrees out at sunrise, by how many degrees did the temperature rise by noon? Since N is negative, the answer to this question has to be positive, and more than 6. | |
\( \large -N\) Hint: If N is negative, then -N is positive | |
\( \large 6+N\) Hint: For example, if \(N=-10\), then \(6+N = -4\) |
Question 9 |
There are 15 students for every teacher. Let t represent the number of teachers and let s represent the number of students. Which of the following equations is correct?
\( \large t=s+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large s=t+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large t=15s\) Hint: This is a really easy mistake to make, which comes from transcribing directly from English, "1 teachers equals 15 students." To see that it's wrong, plug in s=2; do you really need 30 teachers for 2 students? To avoid this mistake, insert the word "number," "Number of teachers equals 15 times number of students" is more clearly problematic. | |
\( \large s=15t\) |
Question 10 |
Here are some statements:
I) 5 is an integer II)\( -5 \) is an integer III) \(0\) is an integer
Which of the statements are true?
I only | |
I and II only | |
I and III only | |
I, II, and IIIHint: The integers are ...-3, -2, -1, 0, 1, 2, 3, .... |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.