Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
Here is a number trick:
1) Pick a whole number
2) Double your number.
3) Add 20 to the above result.
4) Multiply the above by 5
5) Subtract 100
6) Divide by 10
The result is always the number that you started with! Suppose you start by picking N. Which of the equations below best demonstrates that the result after Step 6 is also N?
\( \large N*2+20*5-100\div 10=N\) Hint: Use parentheses or else order of operations is off. | |
\( \large \left( \left( 2*N+20 \right)*5-100 \right)\div 10=N\) | |
\( \large \left( N+N+20 \right)*5-100\div 10=N\) Hint: With this answer you would subtract 10, instead of subtracting 100 and then dividing by 10. | |
\( \large \left( \left( \left( N\div 10 \right)-100 \right)*5+20 \right)*2=N\) Hint: This answer is quite backwards. |
Question 2 |
Which of the lists below is in order from least to greatest value?
\( \large -0.044,\quad -0.04,\quad 0.04,\quad 0.044\) Hint: These are easier to compare if you add trailing zeroes (this is finding a common denominator) -- all in thousandths, -0.044, -0.040,0 .040, 0.044. The middle two numbers, -0.040 and 0.040 can be modeled as owing 4 cents and having 4 cents. The outer two numbers are owing or having a bit more. | |
\( \large -0.04,\quad -0.044,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. | |
\( \large -0.04,\quad -0.044,\quad 0.04,\quad 0.044\) Hint: -0.04=-0.040, which is greater than \(-0.044\). | |
\( \large -0.044,\quad -0.04,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. |
Question 3 |
Which of the lists below contains only irrational numbers?
\( \large\pi , \quad \sqrt{6},\quad \sqrt{\dfrac{1}{2}}\) | |
\( \large\pi , \quad \sqrt{9}, \quad \pi +1\) Hint: \( \sqrt{9}=3\) | |
\( \large\dfrac{1}{3},\quad \dfrac{5}{4},\quad \dfrac{2}{9}\) Hint: These are all rational. | |
\( \large-3,\quad 14,\quad 0\) Hint: These are all rational. |
Question 4 |
What is the probability that two randomly selected people were born on the same day of the week? Assume that all days are equally probable.
\( \large \dfrac{1}{7}\) Hint: It doesn't matter what day the first person was born on. The probability that the second person will match is 1/7 (just designate one person the first and the other the second). Another way to look at it is that if you list the sample space of all possible pairs, e.g. (Wed, Sun), there are 49 such pairs, and 7 of them are repeats of the same day, and 7/49=1/7. | |
\( \large \dfrac{1}{14}\) Hint: What would be the sample space here? Ie, how would you list 14 things that you pick one from? | |
\( \large \dfrac{1}{42}\) Hint: If you wrote the seven days of the week on pieces of paper and put the papers in a jar, this would be the probability that the first person picked Sunday and the second picked Monday from the jar -- not the same situation. | |
\( \large \dfrac{1}{49}\) Hint: This is the probability that they are both born on a particular day, e.g. Sunday. |
Question 5 |
Which of the following inequalities describes all values of x with \(\large \dfrac{x}{2}\le \dfrac{x}{3}\)?
\( \large x < 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \le 0\) | |
\( \large x > 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \ge 0\) Hint: Try plugging in x = 6. |
Question 6 |
Which of the following is equivalent to \( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{2}{8}\times \dfrac{1}{2}?\)
\( \large \dfrac{7}{16}\) Hint: Multiplication comes before addition and subtraction in the order of operations. | |
\( \large \dfrac{1}{2}\) Hint: Addition and subtraction are of equal priority in the order of operations -- do them left to right. | |
\( \large \dfrac{3}{4}\) Hint: \( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{2}{8}\times \dfrac{1}{2}\)=\( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{1}{8}\)=\( \dfrac{3}{4}+-\dfrac{1}{8}+\dfrac{1}{8}\)=\( \dfrac{3}{4}\) | |
\( \large \dfrac{3}{16}\) Hint: Multiplication comes before addition and subtraction in the order of operations. |
Question 7 |
If two fair coins are flipped, what is the probability that one will come up heads and the other tails?
\( \large \dfrac{1}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{3} \) Hint: This is a very common misconception. There are three possible outcomes -- both heads, both tails, and one of each -- but they are not equally likely. Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{2}\) Hint: The possibilities are HH, HT, TH, TT, and all are equally likely. Two of the four have one of each coin, so the probability is 2/4=1/2. | |
\( \large \dfrac{3}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. |
Question 8 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):

Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 9 |
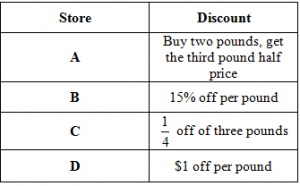
Use the table below to answer the question that follows:
Gordon wants to buy three pounds of nuts. Each of the stores above ordinarily sells the nuts for $4.99 a pound, but is offering a discount this week. At which store can he buy the nuts for the least amount of money?
Store AHint: This would save about $2.50. You can quickly see that D saves more. | |
Store BHint: This saves 15% and C saves 25%. | |
Store C | |
Store DHint: This is about 20% off, which is less of a discount than C. |
Question 10 |
Which of the following is not possible?
An equiangular triangle that is not equilateral.Hint: The AAA property of triangles states that all triangles with corresponding angles congruent are similar. Thus all triangles with three equal angles are similar, and are equilateral. | |
An equiangular quadrilateral that is not equilateral.Hint: A rectangle is equiangular (all angles the same measure), but if it's not a square, it's not equilateral (all sides the same length). | |
An equilateral quadrilateral that is not equiangular.Hint: This rhombus has equal sides, but it doesn't have equal angles:  | |
An equiangular hexagon that is not equilateral.Hint: This hexagon has equal angles, but it doesn't have equal sides: 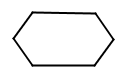 |
Question 11 |
The expression \( \large {{7}^{-4}}\cdot {{8}^{-6}}\) is equal to which of the following?
\( \large \dfrac{8}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 8? | |
\( \large \dfrac{64}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 64? | |
\( \large \dfrac{1}{8\cdot {{\left( 56 \right)}^{4}}}\) Hint: \(8^{-6}=8^{-4} \times 8^{-2}\) | |
\( \large \dfrac{1}{64\cdot {{\left( 56 \right)}^{4}}}\) |
Question 12 |
What is the mathematical name of the three-dimensional polyhedron depicted below?

TetrahedronHint: All the faces of a tetrahedron are triangles. | |
Triangular PrismHint: A prism has two congruent, parallel bases, connected by parallelograms (since this is a right prism, the parallelograms are rectangles). | |
Triangular PyramidHint: A pyramid has one base, not two. | |
TrigonHint: A trigon is a triangle (this is not a common term). |
Question 13 |
Which of the following values of x satisfies the inequality \( \large \left| {{(x+2)}^{3}} \right|<3?\)
\( \large x=-3\) Hint: \( \left| {{(-3+2)}^{3}} \right|\)=\( \left | {(-1)}^3 \right | \)=\( \left | -1 \right |=1 \) . | |
\( \large x=0\) Hint: \( \left| {{(0+2)}^{3}} \right|\)=\( \left | {2}^3 \right | \)=\( \left | 8 \right | \) =\( 8\) | |
\( \large x=-4\) Hint: \( \left| {{(-4+2)}^{3}} \right|\)=\( \left | {(-2)}^3 \right | \)=\( \left | -8 \right | \) =\( 8\) | |
\( \large x=1\) Hint: \( \left| {{(1+2)}^{3}} \right|\)=\( \left | {3}^3 \right | \)=\( \left | 27 \right | \) = \(27\) |
Question 14 |
Each individual cube that makes up the rectangular solid depicted below has 6 inch sides. What is the surface area of the solid in square feet?

\( \large 11\text{ f}{{\text{t}}^{2}}\) Hint: Check your units and make sure you're using feet and inches consistently. | |
\( \large 16.5\text{ f}{{\text{t}}^{2}}\) Hint: Each square has surface area \(\dfrac{1}{2} \times \dfrac {1}{2}=\dfrac {1}{4}\) sq feet. There are 9 squares on the top and bottom, and 12 on each of 4 sides, for a total of 66 squares. 66 squares \(\times \dfrac {1}{4}\) sq feet/square =16.5 sq feet. | |
\( \large 66\text{ f}{{\text{t}}^{2}}\) Hint: The area of each square is not 1. | |
\( \large 2376\text{ f}{{\text{t}}^{2}}\) Hint: Read the question more carefully -- the answer is supposed to be in sq feet, not sq inches.
|
Question 15 |
Use the solution procedure below to answer the question that follows:
\( \large {\left( x+3 \right)}^{2}=10\)
\( \large \left( x+3 \right)\left( x+3 \right)=10\)
\( \large {x}^{2}+9=10\)
\( \large {x}^{2}+9-9=10-9\)
\( \large {x}^{2}=1\)
\( \large x=1\text{ or }x=-1\)
Which of the following is incorrect in the procedure shown above?
The commutative property is used incorrectly.Hint: The commutative property is \(a+b=b+a\) or \(ab=ba\). | |
The associative property is used incorrectly.Hint: The associative property is \(a+(b+c)=(a+b)+c\) or
\(a \times (b \times c)=(a \times b) \times c\). | |
Order of operations is done incorrectly. | |
The distributive property is used incorrectly.Hint: \((x+3)(x+3)=x(x+3)+3(x+3)\)=\(x^2+3x+3x+9.\) |
Question 16 |
The polygon depicted below is drawn on dot paper, with the dots spaced 1 unit apart. What is the perimeter of the polygon?

\( \large 18+\sqrt{2} \text{ units}\) Hint: Be careful with the Pythagorean Theorem. | |
\( \large 18+2\sqrt{2}\text{ units}\) Hint: There are 13 horizontal or vertical 1 unit segments. The longer diagonal is the hypotenuse of a 3-4-5 right triangle, so its length is 5 units. The shorter diagonal is the hypotenuse of a 45-45-90 right triangle with side 2, so its hypotenuse has length \(2 \sqrt{2}\). | |
\( \large 18 \text{ units}
\) Hint: Use the Pythagorean Theorem to find the lengths of the diagonal segments. | |
\( \large 20 \text{ units}\) Hint: Use the Pythagorean Theorem to find the lengths of the diagonal segments. |
Question 17 |
A publisher prints a series of books with covers made of identical material and using the same thickness of paper for each page. The covers of the book together are 0.4 cm thick, and 125 pieces of the paper used together are 1 cm thick.
The publisher uses a linear function to determine the total thickness, T(n) of a book made with n sheets of paper. What are the slope and intercept of T(n)?
Intercept = 0.4 cm, Slope = 125 cm/pageHint: This would mean that each page of the book was 125 cm thick. | |
Intercept =0.4 cm, Slope = \(\dfrac{1}{125}\)cm/pageHint: The intercept is how thick the book would be with no pages in it. The slope is how much 1 extra page adds to the thickness of the book. | |
Intercept = 125 cm, Slope = 0.4 cmHint: This would mean that with no pages in the book, it would be 125 cm thick. | |
Intercept = \(\dfrac{1}{125}\)cm, Slope = 0.4 pages/cmHint: This would mean that each new page of the book made it 0.4 cm thicker. |
Question 18 |
Below is a portion of a number line:

Point B is halfway between two tick marks. What number is represented by Point B?
\( \large 0.645\) Hint: That point is marked on the line, to the right. | |
\( \large 0.6421\) Hint: That point is to the left of point B. | |
\( \large 0.6422\) Hint: That point is to the left of point B. | |
\( \large 0.6425\) |
Question 19 |
On a map the distance from Boston to Detroit is 6 cm, and these two cities are 702 miles away from each other. Assuming the scale of the map is the same throughout, which answer below is closest to the distance between Boston and San Francisco on the map, given that they are 2,708 miles away from each other?
21 cmHint: How many miles would correspond to 24 cm on the map? Try adjusting from there. | |
22 cmHint: How many miles would correspond to 24 cm on the map? Try adjusting from there. | |
23 cmHint: One way to solve this without a calculator is to note that 4 groups of 6 cm is 2808 miles, which is 100 miles too much. Then 100 miles would be about 1/7 th of 6 cm, or about 1 cm less than 24 cm. | |
24 cmHint: 4 groups of 6 cm is over 2800 miles on the map, which is too much. |
Question 20 |
How many lines of reflective symmetry and how many centers of rotational symmetry does the parallelogram depicted below have?

4 lines of reflective symmetry, 1 center of rotational symmetry.Hint: Try cutting out a shape like this one from paper, and fold where you think the lines of reflective symmetry are (or put a mirror there). Do things line up as you thought they would? | |
2 lines of reflective symmetry, 1 center of rotational symmetry.Hint: Try cutting out a shape like this one from paper, and fold where you think the lines of reflective symmetry are (or put a mirror there). Do things line up as you thought they would? | |
0 lines of reflective symmetry, 1 center of rotational symmetry.Hint: The intersection of the diagonals is a center of rotational symmetry. There are no lines of reflective symmetry, although many people get confused about this fact (best to play with hands on examples to get a feel). Just fyi, the letter S also has rotational, but not reflective symmetry, and it's one that kids often write backwards. | |
2 lines of reflective symmetry, 0 centers of rotational symmetry.Hint: Try cutting out a shape like this one from paper. Trace onto another sheet of paper. See if there's a way to rotate the cut out shape (less than a complete turn) so that it fits within the outlines again. |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.