Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
AHint: \(\frac{34}{135} \approx \frac{1}{4}\) and \( \frac{53}{86} \approx \frac {2}{3}\). \(\frac {1}{4}\) of \(\frac {2}{3}\) is small and closest to A. | |
BHint: Estimate with simpler fractions. | |
CHint: Estimate with simpler fractions. | |
DHint: Estimate with simpler fractions. |
Question 2 |
The expression \( \large{{8}^{3}}\cdot {{2}^{-10}}\) is equal to which of the following?
\( \large 2\) Hint: Write \(8^3\) as a power of 2. | |
\( \large \dfrac{1}{2}\) Hint: \(8^3 \cdot {2}^{-10}={(2^3)}^3 \cdot {2}^{-10}\) =\(2^9 \cdot {2}^{-10} =2^{-1}\) | |
\( \large 16\) Hint: Write \(8^3\) as a power of 2. | |
\( \large \dfrac{1}{16}\) Hint: Write \(8^3\) as a power of 2. |
Question 3 |
A family has four children. What is the probability that two children are girls and two are boys? Assume the the probability of having a boy (or a girl) is 50%.
\( \large \dfrac{1}{2}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{4}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{5}\) Hint: Some configurations are more probable than others -- i.e. it's more likely to have two boys and two girls than all boys. Be sure you are weighting properly. | |
\( \large \dfrac{3}{8}\) Hint: There are two possibilities for each child, so there are \(2 \times 2 \times 2 \times 2 =16\) different configurations, e.g. from oldest to youngest BBBG, BGGB, GBBB, etc. Of these configurations, there are 6 with two boys and two girls (this is the combination \(_{4}C_{2}\) or "4 choose 2"): BBGG, BGBG, BGGB, GGBB, GBGB, and GBBG. Thus the probability is 6/16=3/8. |
Question 4 |
The Americans with Disabilties Act (ADA) regulations state that the maximum slope for a wheelchair ramp in new construction is 1:12, although slopes between 1:16 and 1:20 are preferred. The maximum rise for any run is 30 inches. The graph below shows the rise and runs of four different wheelchair ramps. Which ramp is in compliance with the ADA regulations for new construction?

AHint: Rise is more than 30 inches. | |
BHint: Run is almost 24 feet, so rise can be almost 2 feet. | |
CHint: Run is 12 feet, so rise can be at most 1 foot. | |
DHint: Slope is 1:10 -- too steep. |
Question 5 |
Use the expression below to answer the question that follows.
\(\large \dfrac{\left( 155 \right)\times \left( 6,124 \right)}{977}\)
Which of the following is the best estimate of the expression above?
100Hint: 6124/977 is approximately 6. | |
200Hint: 6124/977 is approximately 6. | |
1,000Hint: 6124/977 is approximately 6. 155 is approximately 150, and \( 6 \times 150 = 3 \times 300 = 900\), so this answer is closest. | |
2,000Hint: 6124/977 is approximately 6. |
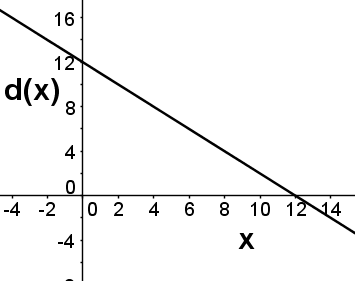
Question 6 |
Use the graph below to answer the question that follows.

Which of the following is a correct equation for the graph of the line depicted above?
\( \large y=-\dfrac{1}{2}x+2\) Hint: The slope is -1/2 and the y-intercept is 2. You can also try just plugging in points. For example, this is the only choice that gives y=1 when x=2. | |
\( \large 4x=2y\) Hint: This line goes through (0,0); the graph above does not. | |
\( \large y=x+2\) Hint: The line pictured has negative slope. | |
\( \large y=-x+2\) Hint: Try plugging x=4 into this equation and see if that point is on the graph above. |
Question 7 |
Which of the numbers below is the decimal equivalent of \( \dfrac{3}{8}?\)
0.38Hint: If you are just writing the numerator next to the denominator then your technique is way off, but by coincidence your answer is close; try with 2/3 and 0.23 is nowhere near correct. | |
0.125Hint: This is 1/8, not 3/8. | |
0.375 | |
0.83Hint: 3/8 is less than a half, and 0.83 is more than a half, so they can't be equal. |
Question 8 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):

Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 9 |
The expression \( \large {{7}^{-4}}\cdot {{8}^{-6}}\) is equal to which of the following?
\( \large \dfrac{8}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 8? | |
\( \large \dfrac{64}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 64? | |
\( \large \dfrac{1}{8\cdot {{\left( 56 \right)}^{4}}}\) Hint: \(8^{-6}=8^{-4} \times 8^{-2}\) | |
\( \large \dfrac{1}{64\cdot {{\left( 56 \right)}^{4}}}\) |
Question 10 |
A solution requires 4 ml of saline for every 7 ml of medicine. How much saline would be required for 50 ml of medicine?
\( \large 28 \dfrac{4}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. The extra ml of saline requires 4 ml saline/ 7 ml medicine = 4/7 ml saline per 1 ml medicine. | |
\( \large 28 \dfrac{1}{4}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 28 \dfrac{1}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 87.5\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? |
Question 11 |
Below is a portion of a number line.

Point A is one-quarter of the distance from 0.26 to 0.28. What number is represented by point A?
\( \large0.26\) Hint: Please reread the question. | |
\( \large0.2625\) Hint: This is one-quarter of the distance between 0.26 and 0.27, which is not what the question asked. | |
\( \large0.265\) | |
\( \large0.27\) Hint: Please read the question more carefully. This answer would be correct if Point A were halfway between the tick marks, but it's not. |
Question 12 |
The function d(x) gives the result when 12 is divided by x. Which of the following is a graph of d(x)?
 Hint: d(x) is 12 divided by x, not x divided by 12. | |
 Hint: When x=2, what should d(x) be? | |
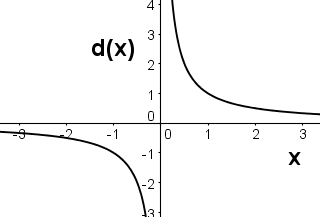 Hint: When x=2, what should d(x) be? | |
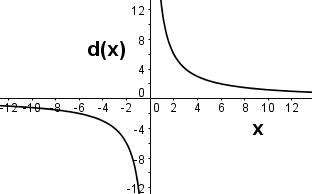 |
Question 13 |
P is a prime number that divides 240. Which of the following must be true?
P divides 30Hint: 2, 3, and 5 are the prime factors of 240, and all divide 30. | |
P divides 48Hint: P=5 doesn't work. | |
P divides 75Hint: P=2 doesn't work. | |
P divides 80Hint: P=3 doesn't work. |
Question 14 |
Aya and Kendra want to estimate the height of a tree. On a sunny day, Aya measures Kendra's shadow as 3 meters long, and Kendra measures the tree's shadow as 15 meters long. Kendra is 1.5 meters tall. How tall is the tree?
7.5 metersHint: Here is a picture, note that the large and small right triangles are similar:  One way to do the problem is to note that there is a dilation (scale) factor of 5 on the shadows, so there must be that factor on the heights too. Another way is to note that the shadows are twice as long as the heights. | |
22.5 metersHint: Draw a picture. | |
30 metersHint: Draw a picture. | |
45 metersHint: Draw a picture. |
Question 15 |
The letters A, B, and C represent digits (possibly equal) in the twelve digit number x=111,111,111,ABC. For which values of A, B, and C is x divisible by 40?
\( \large A = 3, B = 2, C=0\) Hint: Note that it doesn't matter what the first 9 digits are, since 1000 is divisible by 40, so DEF,GHI,JKL,000 is divisible by 40 - we need to check the last 3. | |
\( \large A = 0, B = 0, C=4\) Hint: Not divisible by 10, since it doesn't end in 0. | |
\( \large A = 4, B = 2, C=0\) Hint: Divisible by 10 and by 4, but not by 40, as it's not divisible by 8. Look at 40 as the product of powers of primes -- 8 x 5, and check each. To check 8, either check whether 420 is divisible by 8, or take ones place + twice tens place + 4 * hundreds place = 18, which is not divisible by 8. | |
\( \large A =1, B=0, C=0\) Hint: Divisible by 10 and by 4, but not by 40, as it's not divisible by 8. Look at 40 as the product of powers of primes -- 8 x 5, and check each. To check 8, either check whether 100 is divisible by 8, or take ones place + twice tens place + 4 * hundreds place = 4, which is not divisible by 8. |
Question 16 |
A homeowner is planning to tile the kitchen floor with tiles that measure 6 inches by 8 inches. The kitchen floor is a rectangle that measures 10 ft by 12 ft, and there are no gaps between the tiles. How many tiles does the homeowner need?
30Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. Also, remember that 1 sq foot is 12 \(\times\) 12=144 sq inches. | |
120Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. | |
300Hint: Recheck your calculations. | |
360Hint: One way to do this is to note that 6 inches = 1/2 foot and 8 inches = 2/3 foot, so the area of each tile is 1/2 \(\times\) 2/3=1/3 sq foot, or each square foot of floor requires 3 tiles. The area of the floor is 120 square feet. Note that the tiles would fit evenly oriented in either direction, parallel to the walls. |
Question 17 |
A family on vacation drove the first 200 miles in 4 hours and the second 200 miles in 5 hours. Which expression below gives their average speed for the entire trip?
\( \large \dfrac{200+200}{4+5}\) Hint: Average speed is total distance divided by total time. | |
\( \large \left( \dfrac{200}{4}+\dfrac{200}{5} \right)\div 2\) Hint: This seems logical, but the problem is that it weights the first 4 hours and the second 5 hours equally, when each hour should get the same weight in computing the average speed. | |
\( \large \dfrac{200}{4}+\dfrac{200}{5} \) Hint: This would be an average of 90 miles per hour! | |
\( \large \dfrac{400}{4}+\dfrac{400}{5} \) Hint: This would be an average of 180 miles per hour! Even a family of race car drivers probably doesn't have that average speed on a vacation! |
Question 18 |
Some children explored the diagonals in 2 x 2 squares on pages of a calendar (where all four squares have numbers in them). They conjectured that the sum of the diagonals is always equal; in the example below, 8+16=9+15.
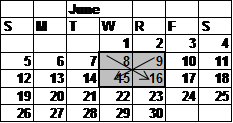
Which of the equations below could best be used to explain why the children's conjecture is correct?
\( \large 8x+16x=9x+15x\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. | |
\( \large x+(x+2)=(x+1)+(x+1)\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. | |
\( \large x+(x+8)=(x+1)+(x+7)\) Hint: x is the number in the top left square, x+8 is one below and to the right, x+1 is to the right of x, and x+7 is below x. | |
\( \large x+8+16=x+9+15\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. |
Question 19 |
Which of the following nets will not fold into a cube?
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
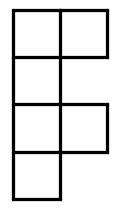 | |
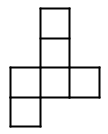 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). |
Question 20 |
Which of the following is the equation of a linear function?
\( \large y={{x}^{2}}+2x+7\) Hint: This is a quadratic function. | |
\( \large y={{2}^{x}}\) Hint: This is an exponential function. | |
\( \large y=\dfrac{15}{x}\) Hint: This is an inverse function. | |
\( \large y=x+(x+4)\) Hint: This is a linear function, y=2x+4, it's graph is a straight line with slope 2 and y-intercept 4. |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.
