The Farey Sequence, \(F_{n}\) is the list of all simplified fractions between \(\dfrac{0}{1}\) and \(\dfrac{1}{1}\) with denominator less than or equal to \(n\). For example,
\( \large F_{5}=\dfrac{0}{1},\dfrac{1}{5},\dfrac{1}{4},\dfrac{1}{3},\dfrac{2}{5},\dfrac{1}{2},\dfrac{3}{5},\dfrac{2}{3},\dfrac{3}{4},\dfrac{4}{5},\dfrac{1}{1}\)
There are many wonderful numerical patterns in the Farey Sequences, and if you have not explored them before, I encourage you to play with the numbers and to see what you can discover.
Below is an applet that shows the first few Farey Sequences on a number line, which is split, both so it fits in this column and to show the symmetry in the Farey Fractions. Move the slider to change the maximum denominator. Click here to see an applet where the number line is not split.
Note that the spacing between the fractions on the number line varies. In order to explore the spacing visually in two dimensions, I made the following applet (which also doesn’t fit well in this column).
The applet plots points \( \left( \dfrac{x}{y},y \right)\), when \( \dfrac{x}{y}\) is in simplest form. Thus, each time the denominator is increased, the Farey Fractions with denominator \(y\) are added at height \(y\).
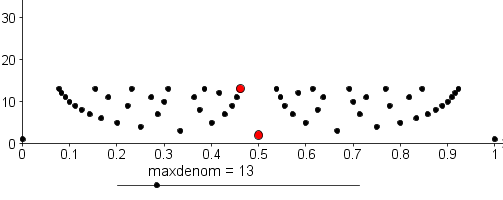
The screenshot below shows the starting screen with two points highlighted in red:
The highlighted points are \(\left( \dfrac{1}{2},2 \right)\) and \(\left( \dfrac{6}{13},13 \right)\). The points corresponding to the Farey Fractions \( \dfrac{1}{2}\) and \( \dfrac{6}{13}\) are in the correct horizontal position on the number line, and the denominators determine their vertical positions.
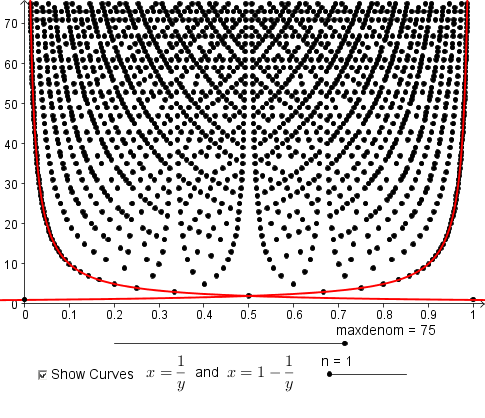
It’s fun to slowly increase the maximum denominator and watch the points fill in. The final picture looks like this:
Note the many visual patterns in the picture. One pattern is that fractions with the same numerator form visible curves (hyperbolas). Checking the “Show Curves” box on the applet allows you to explore this family of curves. Here is a screenshot for fractions with numerator \(1\), as well as fractions where the numerator is one less than the denominator:
As you move the slider to change the numerator, notice that some hyperbolas have more points on them than others. Why?
There are other families of curves that you can explore by entering equations into the input bar. In order to make the graph of the pattern match the number line, many of these equations are easier to see as functions of \(x\) not of \(y\).
GeoGebra accepts implicit equations to graph, but not if \(y\) is in the denominator. So, for example, we might note that the fractions just preceding \(\dfrac{1}{2}\) in the various Farey Sequences are \(\dfrac{1}{3},\dfrac{2}{5},\dfrac{3}{7},\dfrac{4}{9}…\)\(=\dfrac{\dfrac{y-1}{2}}{y}=\dfrac{y-1}{2y}\). Thus our equation is \(x=\dfrac{y-1}{2y}\), which we must simplify, for example, to \(2xy=y-1\), so that there is no \(y\) in the denominator. The \(xy\) term can be entered into GeoGebra as “x y” (with a space in between the variables and no quotes) or as “x*y”. Try entering that curve, and also testing others.
Note that if you don’t want the negative branch of this hyperbola, you can enter the equation as “If[y>0,2 x y = y-1]” — that’s what I did for the curves built into the applet.
You can right click on a curve and choose “Object Properties” to change its color, thickness, etc. Clicking the refresh button in the upper right corner resets everything.
I got the idea for the pattern applet partly from a very interesting book I’ve been reading, A Motif of Mathematics: History and Applications of the Mediant and the Farey Sequences, by Scott B. Guthery (the picture on page 166 is a lot like the one in the applet).
I found it surprising that the introduction of tables for converting between fractions and decimals led people to notice patterns in Farey Fractions. In the early 19th century, when France was switching to the metric system, Charles Haros, a government worker, published a table of decimal equivalents for all simplified fractions with denominator less than 100, i.e. \(F_{100}\). The patterns he found allowed him to write all the fractions in order, and he published a paper describing his algorithms and why they worked.
About fifteen years later, John Farey, a British geologist who had no knowledge of Haros’s work, wrote a note to a journal about a pattern he had noticed in a British table of fraction and decimal equivalents, wondering if it had been pointed out before. Augustin-Louis Cauchy, a very famous mathematician, saw the note and wrote a paper proving the results; he named the sequences after Farey.
G.H. Hardy, a famous 20th century British Mathematician, who in 1938 co-authored a widely read number theory book, was rather disparaging of Farey in the book, saying, “He gave no proof, and it is unlikely that he had found one, as he seems to have been at the best an indifferent mathematician” (page 36 in the 1983 ed.). However, according to Guthery, Farey was a top notch geologist, before the field really existed. My guess is that Hardy himself was likely at best an indifferent geologist.
I rather like the idea that the Farey Sequences are named after someone who noticed a pattern and asked a question — and not even the first person to notice the pattern, ask the question, or even provide the answer. As math teachers, we teach plenty of indifferent mathematicians who wake up when they experience the joy of discovering something that is new to them, not necessarily new to the whole world. Cauchy certainly has plenty of things named after him. Haros definitely has more claim to the sequence than Farey, although the book gives a history that also goes back even further than his work.
For more on visual patterns in Farey Fractions, see this article by Ralph E. Griswold about using Farey Fractions to design patterns for weaving.

Fractions, Sam Loyd, and a MArTH Journal « Math Munch
[…] Fractions, you ask? Debra writes all about them and the cool visual patterns they make in this post. To make a list of Farey Fractions you first pick a number – say, 5. Then, you list all […]
Mel Jane C. de Vera
Hi!!Good day to you!I want to ask if somehow you know the pattern, did you also study about the formula of finding how many Farey fractions are there in a sequence, say 100?
dborkovitz
Sorry for the late response. The number of Farey Fractions of a given denominator is given by the Euler Phi Function (see http://en.wikipedia.org/wiki/Euler's_totient_function), which is connected to a lot of important things in number theory.
Thanks for commenting!