Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time. To see ten new questions, reload the page.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
What is the mathematical name of the three-dimensional polyhedron depicted below?

TetrahedronHint: All the faces of a tetrahedron are triangles. | |
Triangular PrismHint: A prism has two congruent, parallel bases, connected by parallelograms (since this is a right prism, the parallelograms are rectangles). | |
Triangular PyramidHint: A pyramid has one base, not two. | |
TrigonHint: A trigon is a triangle (this is not a common term). |
Question 2 |
The function d(x) gives the result when 12 is divided by x. Which of the following is a graph of d(x)?
 Hint: d(x) is 12 divided by x, not x divided by 12. | |
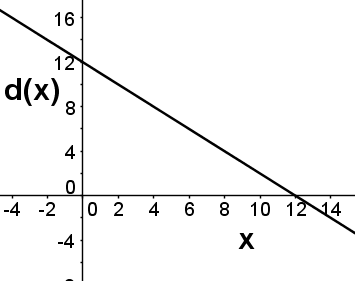 Hint: When x=2, what should d(x) be? | |
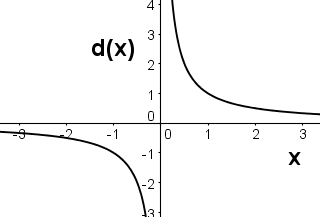 Hint: When x=2, what should d(x) be? | |
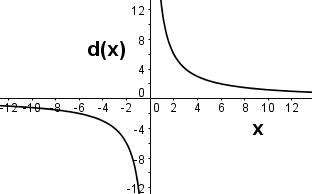 |
Question 3 |
The letters A, B, and C represent digits (possibly equal) in the twelve digit number x=111,111,111,ABC. For which values of A, B, and C is x divisible by 40?
\( \large A = 3, B = 2, C=0\) Hint: Note that it doesn't matter what the first 9 digits are, since 1000 is divisible by 40, so DEF,GHI,JKL,000 is divisible by 40 - we need to check the last 3. | |
\( \large A = 0, B = 0, C=4\) Hint: Not divisible by 10, since it doesn't end in 0. | |
\( \large A = 4, B = 2, C=0\) Hint: Divisible by 10 and by 4, but not by 40, as it's not divisible by 8. Look at 40 as the product of powers of primes -- 8 x 5, and check each. To check 8, either check whether 420 is divisible by 8, or take ones place + twice tens place + 4 * hundreds place = 18, which is not divisible by 8. | |
\( \large A =1, B=0, C=0\) Hint: Divisible by 10 and by 4, but not by 40, as it's not divisible by 8. Look at 40 as the product of powers of primes -- 8 x 5, and check each. To check 8, either check whether 100 is divisible by 8, or take ones place + twice tens place + 4 * hundreds place = 4, which is not divisible by 8. |
Question 4 |
There are 15 students for every teacher. Let t represent the number of teachers and let s represent the number of students. Which of the following equations is correct?
\( \large t=s+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large s=t+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large t=15s\) Hint: This is a really easy mistake to make, which comes from transcribing directly from English, "1 teachers equals 15 students." To see that it's wrong, plug in s=2; do you really need 30 teachers for 2 students? To avoid this mistake, insert the word "number," "Number of teachers equals 15 times number of students" is more clearly problematic. | |
\( \large s=15t\) |
Question 5 |
Here are some statements:
I) 5 is an integer II)\( -5 \) is an integer III) \(0\) is an integer
Which of the statements are true?
I only | |
I and II only | |
I and III only | |
I, II, and IIIHint: The integers are ...-3, -2, -1, 0, 1, 2, 3, .... |
Question 6 |
Which of the following is equal to one million three hundred thousand?
\(\large1.3\times {{10}^{6}}\)
| |
\(\large1.3\times {{10}^{9}}\)
Hint: That's one billion three hundred million. | |
\(\large1.03\times {{10}^{6}}\)
Hint: That's one million thirty thousand. | |
\(\large1.03\times {{10}^{9}}\) Hint: That's one billion thirty million |
Question 7 |
Which of the following inequalities describes all values of x with \(\large \dfrac{x}{2}\le \dfrac{x}{3}\)?
\( \large x < 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \le 0\) | |
\( \large x > 0\) Hint: If x =0, then x/2 = x/3, so this answer can't be correct. | |
\( \large x \ge 0\) Hint: Try plugging in x = 6. |
Question 8 |
Solve for x: \(\large 4-\dfrac{2}{3}x=2x\)
\( \large x=3\) Hint: Try plugging x=3 into the equation. | |
\( \large x=-3\) Hint: Left side is positive, right side is negative when you plug this in for x. | |
\( \large x=\dfrac{3}{2}\) Hint: One way to solve: \(4=\dfrac{2}{3}x+2x\) \(=\dfrac{8}{3}x\).\(x=\dfrac{3 \times 4}{8}=\dfrac{3}{2}\). Another way is to just plug x=3/2 into the equation and see that each side equals 3 -- on a multiple choice test, you almost never have to actually solve for x. | |
\( \large x=-\dfrac{3}{2}\) Hint: Left side is positive, right side is negative when you plug this in for x. |
Question 9 |
The Venn Diagram below gives data on the number of seniors, athletes, and vegetarians in the student body at a college:
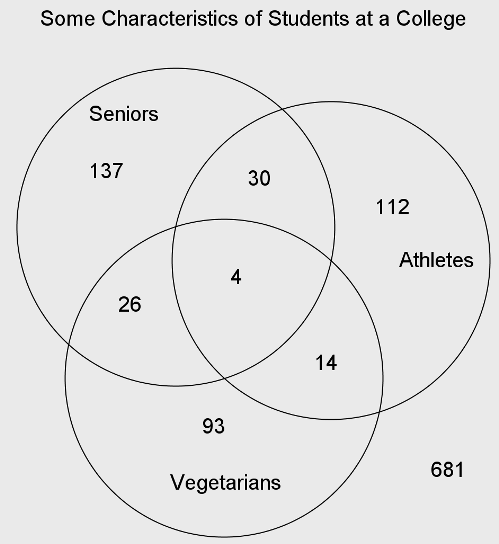
How many students at the college are seniors who are not vegetarians?
\( \large 137\) Hint: Doesn't include the senior athletes who are not vegetarians. | |
\( \large 167\) | |
\( \large 197\) Hint: That's all seniors, including vegetarians. | |
\( \large 279\) Hint: Includes all athletes who are not vegetarians, some of whom are not seniors. |
Question 10 |
Use the graph below to answer the question that follows.

Which of the following is a correct equation for the graph of the line depicted above?
\( \large y=-\dfrac{1}{2}x+2\) Hint: The slope is -1/2 and the y-intercept is 2. You can also try just plugging in points. For example, this is the only choice that gives y=1 when x=2. | |
\( \large 4x=2y\) Hint: This line goes through (0,0); the graph above does not. | |
\( \large y=x+2\) Hint: The line pictured has negative slope. | |
\( \large y=-x+2\) Hint: Try plugging x=4 into this equation and see if that point is on the graph above. |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.