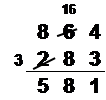Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
In January 2011, the national debt was about 14 trillion dollars and the US population was about 300 million people. Someone reading these figures estimated that the national debt was about $5,000 per person. Which of these statements best describes the reasonableness of this estimate?
It is too low by a factor of 10Hint: 14 trillion \( \approx 15 \times {{10}^{12}} \) and 300 million \( \approx 3 \times {{10}^{8}}\), so the true answer is about \( 5 \times {{10}^{4}} \) or $50,000. | |
It is too low by a factor of 100 | |
It is too high by a factor of 10 | |
It is too high by a factor of 100 |
Question 2 |
What is the mathematical name of the three-dimensional polyhedron depicted below?

TetrahedronHint: All the faces of a tetrahedron are triangles. | |
Triangular PrismHint: A prism has two congruent, parallel bases, connected by parallelograms (since this is a right prism, the parallelograms are rectangles). | |
Triangular PyramidHint: A pyramid has one base, not two. | |
TrigonHint: A trigon is a triangle (this is not a common term). |
Question 3 |
A family has four children. What is the probability that two children are girls and two are boys? Assume the the probability of having a boy (or a girl) is 50%.
\( \large \dfrac{1}{2}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{4}\) Hint: How many different configurations are there from oldest to youngest, e.g. BGGG? How many of them have 2 boys and 2 girls? | |
\( \large \dfrac{1}{5}\) Hint: Some configurations are more probable than others -- i.e. it's more likely to have two boys and two girls than all boys. Be sure you are weighting properly. | |
\( \large \dfrac{3}{8}\) Hint: There are two possibilities for each child, so there are \(2 \times 2 \times 2 \times 2 =16\) different configurations, e.g. from oldest to youngest BBBG, BGGB, GBBB, etc. Of these configurations, there are 6 with two boys and two girls (this is the combination \(_{4}C_{2}\) or "4 choose 2"): BBGG, BGBG, BGGB, GGBB, GBGB, and GBBG. Thus the probability is 6/16=3/8. |
Question 4 |
A sales companies pays its representatives $2 for each item sold, plus 40% of the price of the item. The rest of the money that the representatives collect goes to the company. All transactions are in cash, and all items cost $4 or more. If the price of an item in dollars is p, which expression represents the amount of money the company collects when the item is sold?
\( \large \dfrac{3}{5}p-2\) Hint: The company gets 3/5=60% of the price, minus the $2 per item. | |
\( \large \dfrac{3}{5}\left( p-2 \right)\) Hint: This is sensible, but not what the problem states. | |
\( \large \dfrac{2}{5}p+2\) Hint: The company pays the extra $2; it doesn't collect it. | |
\( \large \dfrac{2}{5}p-2\) Hint: This has the company getting 2/5 = 40% of the price of each item, but that's what the representative gets. |
Question 5 |
A publisher prints a series of books with covers made of identical material and using the same thickness of paper for each page. The covers of the book together are 0.4 cm thick, and 125 pieces of the paper used together are 1 cm thick.
The publisher uses a linear function to determine the total thickness, T(n) of a book made with n sheets of paper. What are the slope and intercept of T(n)?
Intercept = 0.4 cm, Slope = 125 cm/pageHint: This would mean that each page of the book was 125 cm thick. | |
Intercept =0.4 cm, Slope = \(\dfrac{1}{125}\)cm/pageHint: The intercept is how thick the book would be with no pages in it. The slope is how much 1 extra page adds to the thickness of the book. | |
Intercept = 125 cm, Slope = 0.4 cmHint: This would mean that with no pages in the book, it would be 125 cm thick. | |
Intercept = \(\dfrac{1}{125}\)cm, Slope = 0.4 pages/cmHint: This would mean that each new page of the book made it 0.4 cm thicker. |
Question 6 |
Which of the following is an irrational number?
\( \large \sqrt[3]{8}\) Hint: This answer is the cube root of 8. Since 2 x 2 x 2 =8, this is equal to 2, which is rational because 2 = 2/1. | |
\( \large \sqrt{8}\) Hint: It is not trivial to prove that this is irrational, but you can get this answer by eliminating the other choices. | |
\( \large \dfrac{1}{8}\) Hint: 1/8 is the RATIO of two integers, so it is rational. | |
\( \large -8\) Hint: Negative integers are also rational, -8 = -8/1, a ratio of integers. |
Question 7 |
The first histogram shows the average life expectancies for women in different countries in Africa in 1998; the second histogram gives similar data for Europe:
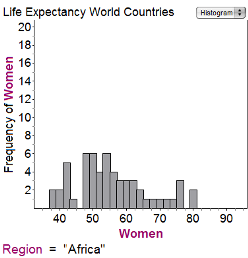

How much bigger is the range of the data for Africa than the range of the data for Europe?
0 yearsHint: Range is the maximum life expectancy minus the minimum life expectancy. | |
12 yearsHint: Are you subtracting frequencies? Range is about values of the data, not frequency. | |
18 yearsHint: It's a little hard to read the graph, but it doesn't matter if you're consistent. It looks like the range for Africa is 80-38= 42 years and for Europe is 88-64 = 24; 42-24=18. | |
42 yearsHint: Read the question more carefully. |
Question 8 |
If x is an integer, which of the following must also be an integer?
\( \large \dfrac{x}{2}\) Hint: If x is odd, then \( \dfrac{x}{2} \) is not an integer, e.g. 3/2 = 1.5. | |
\( \large \dfrac{2}{x}\) Hint: Only an integer if x = -2, -1, 1, or 2. | |
\( \large-x\) Hint: -1 times any integer is still an integer. | |
\(\large\sqrt{x}\) Hint: Usually not an integer, e.g. \( \sqrt{2} \approx 1.414 \). |
Question 9 |
Here is a student's work solving an equation:
\( x-4=-2x+6\)
\( x-4+4=-2x+6+4\)
\( x=-2x+10\)
\( x-2x=10\)
\( x=10\)
Which of the following statements is true?
The student‘s solution is correct.Hint: Try plugging into the original solution. | |
The student did not correctly use properties of equality.Hint: After \( x=-2x+10\), the student subtracted 2x on the left and added 2x on the right. | |
The student did not correctly use the distributive property.Hint: Distributive property is \(a(b+c)=ab+ac\). | |
The student did not correctly use the commutative property.Hint: Commutative property is \(a+b=b+a\) or \(ab=ba\). |
Question 10 |
Here is a mental math strategy for computing 26 x 16:
Step 1: 100 x 16 = 1600
Step 2: 25 x 16 = 1600 ÷· 4 = 400
Step 3: 26 x 16 = 400 + 16 = 416
Which property best justifies Step 3 in this strategy?
Commutative Property.Hint: For addition, the commutative property is \(a+b=b+a\) and for multiplication it's \( a \times b = b \times a\). | |
Associative Property.Hint: For addition, the associative property is \((a+b)+c=a+(b+c)\) and for multiplication it's \((a \times b) \times c=a \times (b \times c)\) | |
Identity Property.Hint: 0 is the additive identity, because \( a+0=a\) and 1 is the multiplicative identity because \(a \times 1=a\). The phrase "identity property" is not standard. | |
Distributive Property.Hint: \( (25+1) \times 16 = 25 \times 16 + 1 \times 16 \). This is an example of the distributive property of multiplication over addition. |
Question 11 |
At a school fundraising event, people can buy a ticket to spin a spinner like the one below. The region that the spinner lands in tells which, if any, prize the person wins.

If 240 people buy tickets to spin the spinner, what is the best estimate of the number of keychains that will be given away?
40Hint: "Keychain" appears on the spinner twice. | |
80Hint: The probability of getting a keychain is 1/3, and so about 1/3 of the time the spinner will win. | |
100Hint: What is the probability of winning a keychain? | |
120Hint: That would be the answer for getting any prize, not a keychain specifically. |
Question 12 |
Given that 10 cm is approximately equal to 4 inches, which of the following expressions models a way to find out approximately how many inches are equivalent to 350 cm?
\( \large 350\times \left( \dfrac{10}{4} \right)\) Hint: The final result should be smaller than 350, and this answer is bigger. | |
\( \large 350\times \left( \dfrac{4}{10} \right)\) Hint: Dimensional analysis can help here: \(350 \text{cm} \times \dfrac{4 \text{in}}{10 \text{cm}}\). The cm's cancel and the answer is in inches. | |
\( \large (10-4) \times 350
\) Hint: This answer doesn't make much sense. Try with a simpler example (e.g. 20 cm not 350 cm) to make sure that your logic makes sense. | |
\( \large (350-10) \times 4\) Hint: This answer doesn't make much sense. Try with a simpler example (e.g. 20 cm not 350 cm) to make sure that your logic makes sense. |
Question 13 |
Four children randomly line up, single file. What is the probability that they are in height order, with the shortest child in front? All of the children are different heights.
\( \large \dfrac{1}{4}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{256}
\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{16}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{24}\) Hint: The number of ways for the children to line up is \(4!=4 \times 3 \times 2 \times 1 =24\) -- there are 4 choices for who is first in line, then 3 for who is second, etc. Only one of these lines has the children in the order specified. |
Question 14 |
Use the graph below to answer the question that follows.

Which of the following is a correct equation for the graph of the line depicted above?
\( \large y=-\dfrac{1}{2}x+2\) Hint: The slope is -1/2 and the y-intercept is 2. You can also try just plugging in points. For example, this is the only choice that gives y=1 when x=2. | |
\( \large 4x=2y\) Hint: This line goes through (0,0); the graph above does not. | |
\( \large y=x+2\) Hint: The line pictured has negative slope. | |
\( \large y=-x+2\) Hint: Try plugging x=4 into this equation and see if that point is on the graph above. |
Question 15 |
The student used a method that worked for this problem and can be generalized to any subtraction problem.Hint: Note that this algorithm is taught as the "standard" algorithm in much of Europe (it's where the term "borrowing" came from -- you borrow on top and "pay back" on the bottom). | |
The student used a method that worked for this problem and that will work for any subtraction problem that only requires one regrouping; it will not work if more regrouping is required.Hint: Try some more examples. | |
The student used a method that worked for this problem and will work for all three-digit subtraction problems, but will not work for larger problems.Hint: Try some more examples. | |
The student used a method that does not work. The student made two mistakes that cancelled each other out and was lucky to get the right answer for this problem.Hint: Remember, there are many ways to do subtraction; there is no one "right" algorithm. |
Question 16 |
Solve for x: \(\large 4-\dfrac{2}{3}x=2x\)
\( \large x=3\) Hint: Try plugging x=3 into the equation. | |
\( \large x=-3\) Hint: Left side is positive, right side is negative when you plug this in for x. | |
\( \large x=\dfrac{3}{2}\) Hint: One way to solve: \(4=\dfrac{2}{3}x+2x\) \(=\dfrac{8}{3}x\).\(x=\dfrac{3 \times 4}{8}=\dfrac{3}{2}\). Another way is to just plug x=3/2 into the equation and see that each side equals 3 -- on a multiple choice test, you almost never have to actually solve for x. | |
\( \large x=-\dfrac{3}{2}\) Hint: Left side is positive, right side is negative when you plug this in for x. |
Question 17 |
Taxicab fares in Boston (Spring 2012) are $2.60 for the first \(\dfrac{1}{7}\) of a mile or less and $0.40 for each \(\dfrac{1}{7}\) of a mile after that.
Let d represent the distance a passenger travels in miles (with \(d>\dfrac{1}{7}\)). Which of the following expressions represents the total fare?
\( \large \$2.60+\$0.40d\) Hint: It's 40 cents for 1/7 of a mile, not per mile. | |
\( \large \$2.60+\$0.40\dfrac{d}{7}\) Hint: According to this equation, going 7 miles would cost $3; does that make sense? | |
\( \large \$2.20+\$2.80d\) Hint: You can think of the fare as $2.20 to enter the cab, and then $0.40 for each 1/7 of a mile, including the first 1/7 of a mile (or $2.80 per mile).
Alternatively, you pay $2.60 for the first 1/7 of a mile, and then $2.80 per mile for d-1/7 miles. The total is 2.60+2.80(d-1/7) = 2.60+ 2.80d -.40 = 2.20+2.80d. | |
\( \large \$2.60+\$2.80d\) Hint: Don't count the first 1/7 of a mile twice. |
Question 18 |
The "houses" below are made of toothpicks and gum drops.
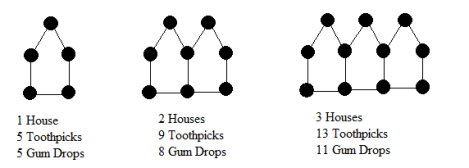
How many toothpicks are there in a row of 53 houses?
212Hint: Can the number of toothpicks be even? | |
213Hint: One way to see this is that every new "house" adds 4 toothpicks to the leftmost vertical toothpick -- so the total number is 1 plus 4 times the number of "houses." There are many other ways to look at the problem too. | |
217Hint: Try your strategy with a smaller number of "houses" so you can count and find your mistake. | |
265Hint: Remember that the "houses" overlap some walls. |
Question 19 |
Below is a portion of a number line:

Point B is halfway between two tick marks. What number is represented by Point B?
\( \large 0.645\) Hint: That point is marked on the line, to the right. | |
\( \large 0.6421\) Hint: That point is to the left of point B. | |
\( \large 0.6422\) Hint: That point is to the left of point B. | |
\( \large 0.6425\) |
Question 20 |
Which of the numbers below is a fraction equivalent to \( 0.\bar{6}\)?
\( \large \dfrac{4}{6}\) Hint: \( 0.\bar{6}=\dfrac{2}{3}=\dfrac{4}{6}\) | |
\( \large \dfrac{3}{5}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice c, which is another way to tell that it's wrong. | |
\( \large \dfrac{6}{10}\) Hint: This is equal to 0.6, without the repeating decimal. Answer is equivalent to choice b, which is another way to tell that it's wrong. | |
\( \large \dfrac{1}{6}\) Hint: This is less than a half, and \( 0.\bar{6}\) is greater than a half. |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.