Which is bigger, the sine of 40\(^{\circ}\) or the sine of 50\(^{\circ}\)?
This is a great trigonometry assessment question. Unfortunately, virtually none of my college students who haven’t used trig for a while can answer it (without a calculator). For a lot of students, trig is one of those subjects that just didn’t stick very well.
So, we start trig functions all over, but this time with circle definitions and some “trigonometry yoga” (no trademark; I made up the name when I was thinking of a title for this post).
I introduce \((cos\theta,sin\theta)\) as the coordinates of the point on the circumference of a unit circle at angle \(\theta\). I point out that cosine and sine, like x and y, are in alphabetical order, which is one way to remember which is which.
Everyone stands.
We practice: hands over the head, as high up as they can go, represents 1. Hands at waist level represents 0. Hands as low as they can go represents -1.
We start with sine yoga. Hands start at waist level, 0. I start at \(\theta\) = 0 degrees and move my finger counter-clockwise around the circle, while the students move their arms up, corresponding to the height of my finger — up to 1, then down to 0, then down to -1, then back to 0. We go around a few more times. They make waves.
I ask again, which is bigger, sine of 40\(^{\circ}\) or sine of 50\(^{\circ}\). Now everyone can easily answer – their hands are moving up from 0 degrees to 90 degrees, obviously sine of 50\(^{\circ}\) is bigger.
We try some cosine yoga. I start at 0, their hands start up at 1, and then down to 0, down to -1, back up to 0, and back to 1 again. Cosine yoga is a little trickier, but they catch on easily. After a few rounds, cosine looks, well, just like sine, except 90 degrees out of synch.
There’s much more trig yoga we can do – go around the circle twice as fast (or three times or half), go backwards, use a smaller circle (a bigger circle requires longer arms or a change of scale), start in different places, or move the furniture and try a yoga dance with students moving across the room at a constant rate as their arms move up and down (get out some paper and convert this last one to a graph!).
I haven’t actually tried all these trig yoga variations, but I’ll try some more next time I teach this topic.
Before the activity, here’s what most of the students remembered about trig functions: SohCahToa – Sine: Opposite over Hypotenuse; Cosine: Adjacent over Hypotenuse; Tangent: Opposite over Adjacent.
Here’s what they could do with this information: Take a right triangle where they know the sides and find the sine, cosine, and tangent. Or take a right triangle where they know the angles and one side, and find the other two sides.
Here’s what the students who remembered a little more also remembered: Sine and cosine are waves. When you’re graphing a wave, you’re supposed to use radians for some reason, and radians have pi in them and there’s a formula for converting degrees to radians. It’s not so clear what sine waves have to do with the SohCahToa right triangle business.
Students know that answering which is bigger, sine of 40\(^{\circ}\) or 50\(^{\circ}\) should be an easy question, but they haven’t internalized the meaning of trig functions beyond direct application of the memorized mnemonic.
I think the ratio definitions are a big part of the problem. Opposite and Hypotenuse are two different lengths, and defining sine as their ratio means defining sine as a relationship between two variables. Developing intuition about definitions involving ratios is much more difficult than developing intuition about one-variable definitions. Fractions are harder than whole numbers; slopes are harder than distances.
Trigonometry yoga is different from anything my students have seen before, so it’s a way to revisit an old topic without seeming repetitive. It’s silly and fun. Involving the whole body helps students literally get a feel for the definitions. Certainly middle school kids could do trigonometry yoga (elementary kids too). I wonder what it would be like to introduce sine and cosine for the first time this way and to save the SohCahToa for later (or better yet, skip it entirely).
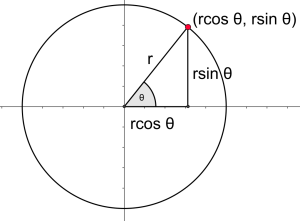
It’s straightforward to derive the triangle definitions of sine and cosine from the circle ones: dilate the unit circle so it has radius \(r\) (or radius \(h\) if you prefer). Now the point on the circle at angle \(\theta\) has coordinates \((r cos\theta,r sin\theta)\).
Draw the right triangle with sides parallel to the axes and with hypotenuse the radius at angle \(\theta\), as shown above. Using this triangle, it’s clear that \(sin\theta\) is equal to Opposite over Hypotenuse, and \(cos \theta\) is equal to Adjacent over Hypotenuse
The above representation shows a vector separated into vertical and horizontal components – another very useful way to look at sine and cosine.
The tangent can be defined as the slope of the line forming angle \(\theta\) with the x-axis, which is another ratio definition, but one that students have at least already seen when they studied slopes. The tangent can also be defined with a geometric, one-variable definition; see my post, The Tangent is a Tangent!
In his excellent article, Historical Reflections on Teaching Trigonometry, David Bressoud writes that circle trigonometry preceded triangle trigonometry by a thousand years, and it wasn’t until the mid to late 1800’s that schools started emphasizing triangles over circles in teaching trigonometry. The article discusses the astronomical calculations of chord lengths that motivated the development of circle trigonometry and the calculations of shadow lengths that later motivated the development of triangle trigonometry. Bressoud advocates introducing trig functions first as lengths of segments in a circle with radius 1, as developed historically before the triangle definitions, and as we do in trigonometry yoga.
So, trigonometry yoga has some historical resonance , although trigonometry predates Cartesian Coordinates by many years, and I don’t think the ancient astronomers who developed it waved their hands up and down to mimic the sine function (but who knows?).
If you try trigonometry yoga with your students, please let me know how it goes.

Colin Beveridge
Nice approach! I might steal this for some of my students :o)
dborkovitz
Thanks! And it’s not stealing if I give it away…. 🙂
Paul McKenzie
Wonderful post. I will try this very natural approach with my grade 9 son tomorrow. It’s a shame my grade 8 students won’t need it this year, but I’ll pass this post along to next year’s teacher. I am certain this approach would have saved me hours and hours of confusion when I was at school – as well as helping me see the bigger picture more clearly. Thanks so much 🙂
dborkovitz
You’re welcome. I haven’t had the chance to try this approach with someone new to trig, so would be very interested to hear how it goes with your son. Appreciate the comment.
Anonymous
That’s a very innovative idea, I am going to try it too with my students
dborkovitz
Thanks for your comment. I’d be interested to hear how it goes with your students.