Last week I read an excerpt in the Boston Globe from the blog post, “How to Improve Boston Public Schools,” by Nicholas C. Donohue, president of the Nellie Mae Educational foundation. The post focused on four items – increasing expectations, advancing students based on their mastery of skills, endorsing learning anywhere, and student-centered learning. Later on, thinking about the post, I was reminded of the “lez-umé,” a concept my friends and I came up with in the 1980’s, when we were in our twenties.
A lez-umé (pronounced, lez–ooo–may, rhymes with “résumé”) was our fantasy résumé, where we included things we couldn’t put on our actual resume: skills learned as activists (sometimes on what are now called GLBT issues, but also in a wide variety of movements), as housemates dealing with the practical and emotional realities of living in a network of group houses, and as people who had experienced, and continued to experience, violence and abuse and who were writing, speaking out, and doing therapy to struggle to cope and work to prevent what had happened to us.
Today I wouldn’t necessarily call these skills “lesbian,” but in the context of the lesbian-feminist communities we were part of at the time, that’s how we thought of them.
By the mid 1990’s, when I applied for my current job, I was able to put a few of my “lez-umé” items on my actual CV, although not the ones that explained what impressed people most about me: how I became a person with a Ph.D. in math from an elite institution who could work with people who were terrified of math. These skills are strongly rooted in my history of abuse and in spending much of my twenties (and beyond) addressing that history. Therapy and activism and depression interfered significantly with my official graduate school mathematics education, but they were integral to preparing me for my current job.
During my long experience with gastrointestinal and other medical issues, I’ve undergone my fair share of painful tests and procedures. I am usually able to breathe and stay calm (something I learned mostly from yoga), and often the doctor will tell me, “You’re doing great,” in a tone similar to the empty praise so common in classrooms. In the medical setting, “doing great” means not interfering with the procedure or annoying the doctor by squirming, screaming, or hitting, and my standard retort has become, “I’ll put that on my resume,” i.e. the resume that I am not building while I am going through these procedures, even though the ability to avoid annoying people who are causing you pain is a sought-after workplace skill.
I think of my history when I read articles like Mr. Donohue’s touting the benefits of competency-based education. In some ways, I’m all for it, but which competencies do we care about? How do we measure them? At what point in time do we measure them? How do we check back to see what faded and what improved over time? And can we do better than “competent?” How about expert? Original? Passionate? Compassionate?
The author’s example under the “Increase our Expectations” heading is one that’s very familiar to me. He states, “Imagine a high-school experience where students learn what the Pythagorean Theorem is and, having used it in a real world setting, understand more deeply what it means.” I truly hope we can increase our expectations a bit more than that, as all middle and high school geometry curricula already include real world contexts for the Pythagorean Theorem, and many, many teachers have their students apply it in real world settings.
I ask my students why the Pythagorean theorem is true, and pretty much no one ever knows, and for most, it’s a jarring question; Pythagoras is true because their teachers told them it’s true. Often asking “why” was discouraged in their math classes, as time-consuming questions made classes get behind on checking off their learning objectives. Many students did in fact see proofs of the Pythagorean Theorem, and perhaps even passed tests on it and demonstrated the “skills” they had on that one test day, but a few years later, the “mastery” does not remain.
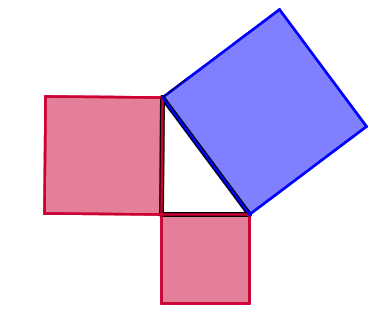
A question with an outcome that’s even less measurable is, “Why is the Pythagorean theorem amazing?” The Pythagorean Theorem is unexpected. I often introduce it with a picture.
I say that the squares are made out of gold, of uniform thickness, and ask which the students would rather have, the two red squares or the blue one. Often students don’t recognize the Pythagorean Theorem right away (and it would be much better if they got this highly impractical question about gold in elementary school, before they’d ever seen the theorem), and there is debate; the answer is not obvious to most. If we’ve convinced ourselves that the payoffs are the same, based on evidence beyond “my teachers said so,” we can delve into some of the hundreds of proofs of the Pythagorean Theorem and learn from them. We can think about other triangles – different shapes of right triangles, acute and obtuse triangles, triangles on a sphere, in 3D coordinates, etc. Is the Pythagorean Theorem true for these triangles? If not, why not? Can it be modified? If so, how do we know? These are the questions that help students understand more deeply what the Pythagorean Theorem means. Last year one of my students devised her own proof of the Pythagorean Theorem – it turned out she wasn’t the first to discover that particular proof, but her joy and pride went well beyond simple measurement of skills.
Currently education is mostly measured in credits which are a function of seat time, which is easy to measure, but is not a unit of learning. I understand the impulse for something better; I agree with it. But even a topic from the existing curriculum as concrete as the Pythagorean Theorem does not easily translate into meaningful measurement of “skill.” Then when move beyond the classroom, as the author describes, “endorsing learning everywhere,” we have to ask, “Just how far we are willing to move?”
The “lez-ume” was a funny rhyme between twenty-somethings a long time ago, but it hints at something much more general: what learning “counts” as learning? Is there a way to acknowledge learning outside the standard curriculum, including learning that is most vital to the student? Or should we just have students watch videos about the Pythagorean Theorem outside of class, take an online quiz, and call that a revolution?
Bill Withers
Thank you for your discussion of the Pythagorean Theorem. I’m pretty sure I’ve seen the 3 squares illustration before, but not nearly (or recently) often enough.
Today a dozen 4th graders built square arrays in sizes ranging from 2×2 through 12×12. They discovered the 3,4,5 combination pretty quickly. A few minutes later they put the 6,8,10 combination together. Then they tried to sketch their squares. I think the sketching was the hardest part for them!
We didn’t bother to name this relationship other than to point out how special it was to find whole numbers that worked in this combination of squares. One little guy stayed after class to (very tentatively) tell me he had seen this before, but he couldn’t remember what it was called. He thought it was “some theorem.” I agreed.
dborkovitz
Sounds like a great class, Bill! Thanks for sharing.
This year with my future elementary teachers, I projected the three squares above, first not arranged in a triangle. They argued about two reds vs. one blue, even measuring the screen w/their forearms and such. Then when I projected the triangle picture, a few made the connection, and we moved to some activities toward justifying the theorem.
Most of the class felt cheated that a teacher had just told them about the Pythagorean Theorem before they got to play with it themselves. Glad your students aren’t being cheated that way!
Ardita
It seems like a great educational patcrice to show students how to prove various equations. When I was in school, I used the equation a^2 + b^2 = c^2, but I do not remember it being explained using pictures. Without the proof, students would be likely to write down the equation, plug numbers in, and solve it, and not understand where it came from or how it was derived. My first physics class in college, labs were assigned where we, students, derived equations. These were equations that I had used in high school, but it was very educational actually seeing how they came about.