Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time. To see ten new questions, reload the page.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):
Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 1 Explanation:
Topic: Recognize and analyze pictorial representations of number operations. (Objective 0019).
Question 2 |
The prime factorization of n can be written as n=pqr, where p, q, and r are distinct prime numbers. How many factors does n have, including 1 and itself?
\( \large3\) Hint: 1, p, q, r, and pqr are already 5, so this isn't enough. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large5\) Hint: Don't forget pq, etc. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large6\) Hint: You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large8\) Hint: 1, p, q, r, pq, pr, qr, pqr. |
Question 2 Explanation:
Topic: Recognize uses of prime factorization of a number (Objective 0018).
Question 3 |
| I. \(\large \dfrac{1}{2}+\dfrac{1}{3}\) | II. \( \large .400000\) | III. \(\large\dfrac{1}{5}+\dfrac{1}{5}\) |
| IV. \( \large 40\% \) | V. \( \large 0.25 \) | VI. \(\large\dfrac{14}{35}\) |
Which of the lists below includes all of the above expressions that are equivalent to \( \dfrac{2}{5}\)?
I, III, V, VIHint: I and V are not at all how fractions and decimals work. | |
III, VIHint: These are right, but there are more. | |
II, III, VIHint: These are right, but there are more. | |
II, III, IV, VI |
Question 3 Explanation:
Topic: Converting between fractions, decimals, and percents (Objective 0017)
Question 4 |
A teacher has a list of all the countries in the world and their populations in March 2012. She is going to have her students use technology to compute the mean and median of the numbers on the list. Which of the following statements is true?
The teacher can be sure that the mean and median will be the same without doing any computation.Hint: Does this make sense? How likely is it that the mean and median of any large data set will be the same? | |
The teacher can be sure that the mean is bigger than the median without doing any computation.Hint: This is a skewed distribution, and very large countries like China and India contribute huge numbers to the mean, but are counted the same as small countries like Luxembourg in the median (the same thing happens w/data on salaries, where a few very high income people tilt the mean -- that's why such data is usually reported as medians). | |
The teacher can be sure that the median is bigger than the mean without doing any computation.Hint: Think about a set of numbers like 1, 2, 3, 4, 10,000 -- how do the mean/median compare? How might that relate to countries of the world? | |
There is no way for the teacher to know the relative size of the mean and median without computing them.Hint: Knowing the shape of the distribution of populations does give us enough info to know the relative size of the mean and median, even without computing them. |
Question 4 Explanation:
Topic: Use measures of central tendency (e.g., mean, median, mode) and
spread to describe and interpret real-world data (Objective 0025).
Question 5 |
Use the problem below to answer the question that follows:
T shirts are on sale for 20% off. Tasha paid $8.73 for a shirt. What is the regular price of the shirt? There is no tax on clothing purchases under $175.
Let p represent the regular price of these t-shirt. Which of the following equations is correct?
\( \large 0.8p=\$8.73\) Hint: 80% of the regular price = $8.73. | |
\( \large \$8.73+0.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice c. | |
\( \large 1.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice b. | |
\( \large p-0.2*\$8.73=p\) Hint: Subtract p from both sides of this equation, and you have -.2 x 8.73 =0. |
Question 5 Explanation:
Topics: Use algebra to solve word problems involving percents and identify variables, and derive algebraic expressions that represent real-world situations (Objective 0020).
Question 6 |
The histogram below shows the number of pairs of footware owned by a group of college students.
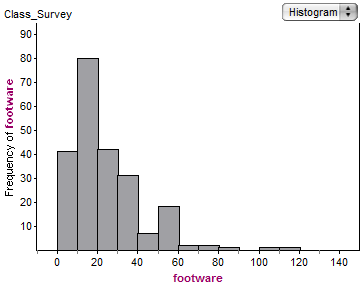
Which of the following statements can be inferred from the graph above?
The median number of pairs of footware owned is between 50 and 60 pairs.Hint: The same number of data points are less than the median as are greater than the median -- but on this histogram, clearly more than half the students own less than 50 pairs of shoes, so the median is less than 50. | |
The mode of the number of pairs of footware owned is 20.Hint: The mode is the most common number of pairs of footwear owned. We can't tell it from this histogram because each bar represents 10 different numbers-- perhaps 8 students each own each number from 10 to 19, but 40 students own exactly 6 pairs of shoes.... or perhaps not.... | |
The mean number of pairs of footware owned is less than the median number of pairs of footware owned.Hint: This is a right skewed distribution, and so the mean is bigger than the median -- the few large values on the right pull up the mean, but have little effect on the median. | |
The median number of pairs of footware owned is between 10 and 20.Hint: There are approximately 230 students represented in this survey, and the 41st through 120th lowest values are between 10 and 20 -- thus the middle value is in that range. |
Question 6 Explanation:
Topics: Analyze and interpret various graphic and data
representations, and use measures of central tendency (e.g., mean, median, mode) and
spread to describe and interpret real-world data (Objective 0025).
Question 7 |
Which of the following is equivalent to \( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{2}{8}\times \dfrac{1}{2}?\)
\( \large \dfrac{7}{16}\) Hint: Multiplication comes before addition and subtraction in the order of operations. | |
\( \large \dfrac{1}{2}\) Hint: Addition and subtraction are of equal priority in the order of operations -- do them left to right. | |
\( \large \dfrac{3}{4}\) Hint: \( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{2}{8}\times \dfrac{1}{2}\)=\( \dfrac{3}{4}-\dfrac{1}{8}+\dfrac{1}{8}\)=\( \dfrac{3}{4}+-\dfrac{1}{8}+\dfrac{1}{8}\)=\( \dfrac{3}{4}\) | |
\( \large \dfrac{3}{16}\) Hint: Multiplication comes before addition and subtraction in the order of operations. |
Question 7 Explanation:
Topic: Operations on Fractions, Order of Operations (Objective 0019).
Question 8 |
The expression \( \large {{7}^{-4}}\cdot {{8}^{-6}}\) is equal to which of the following?
\( \large \dfrac{8}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 8? | |
\( \large \dfrac{64}{{{\left( 56 \right)}^{4}}}\) Hint: The bases are whole numbers, and the exponents are negative. How can the numerator be 64? | |
\( \large \dfrac{1}{8\cdot {{\left( 56 \right)}^{4}}}\) Hint: \(8^{-6}=8^{-4} \times 8^{-2}\) | |
\( \large \dfrac{1}{64\cdot {{\left( 56 \right)}^{4}}}\) |
Question 8 Explanation:
Topics: Laws of exponents (Objective 0019).
Question 9 |
M is a multiple of 26. Which of the following cannot be true?
M is odd.Hint: All multiples of 26 are also multiples of 2, so they must be even. | |
M is a multiple of 3.Hint: 3 x 26 is a multiple of both 3 and 26. | |
M is 26.Hint: 1 x 26 is a multiple of 26. | |
M is 0.Hint: 0 x 26 is a multiple of 26. |
Question 9 Explanation:
Topic: Characteristics of composite numbers (Objective 0018).
Question 10 |
A solution requires 4 ml of saline for every 7 ml of medicine. How much saline would be required for 50 ml of medicine?
\( \large 28 \dfrac{4}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. The extra ml of saline requires 4 ml saline/ 7 ml medicine = 4/7 ml saline per 1 ml medicine. | |
\( \large 28 \dfrac{1}{4}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 28 \dfrac{1}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 87.5\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? |
Question 10 Explanation:
Topic: Apply proportional thinking to estimate quantities in real world situations (Objective 0019).
There are 10 questions to complete.
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.