Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
Four children randomly line up, single file. What is the probability that they are in height order, with the shortest child in front? All of the children are different heights.
\( \large \dfrac{1}{4}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{256}
\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{16}\) Hint: Try a simpler question with 3 children -- call them big, medium, and small -- and list all the ways they could line up. Then see how to extend your logic to the problem with 4 children. | |
\( \large \dfrac{1}{24}\) Hint: The number of ways for the children to line up is \(4!=4 \times 3 \times 2 \times 1 =24\) -- there are 4 choices for who is first in line, then 3 for who is second, etc. Only one of these lines has the children in the order specified. |
Question 2 |
M is a multiple of 26. Which of the following cannot be true?
M is odd.Hint: All multiples of 26 are also multiples of 2, so they must be even. | |
M is a multiple of 3.Hint: 3 x 26 is a multiple of both 3 and 26. | |
M is 26.Hint: 1 x 26 is a multiple of 26. | |
M is 0.Hint: 0 x 26 is a multiple of 26. |
Question 3 |
Use the table below to answer the question that follows:
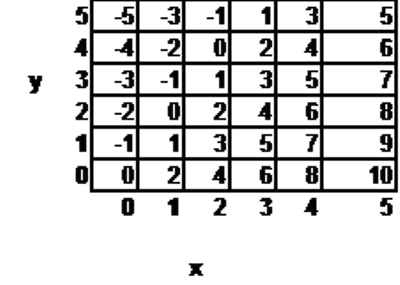
Each number in the table above represents a value W that is determined by the values of x and y. For example, when x=3 and y=1, W=5. What is the value of W when x=9 and y=14? Assume that the patterns in the table continue as shown.
\( \large W=-5\) Hint: When y is even, W is even. | |
\( \large W=4\) Hint: Note that when x increases by 1, W increases by 2, and when y increases by 1, W decreases by 1. At x=y=0, W=0, so at x=9, y=14, W has increased by \(9 \times 2\) and decreased by 14, or W=18-14=4. | |
\( \large W=6\) Hint: Try fixing x or y at 0, and start by finding W for x=0 y=14 or x=9, y=0. | |
\( \large W=32\) Hint: Try fixing x or y at 0, and start by finding W for x=0 y=14 or x=9, y=0. |
Question 4 |
What is the greatest common factor of 540 and 216?
\( \large{{2}^{2}}\cdot {{3}^{3}}\) Hint: One way to solve this is to factor both numbers: \(540=2^2 \cdot 3^3 \cdot 5\) and \(216=2^3 \cdot 3^3\). Then take the smaller power for each prime that is a factor of both numbers. | |
\( \large2\cdot 3\) Hint: This is a common factor of both numbers, but it's not the greatest common factor. | |
\( \large{{2}^{3}}\cdot {{3}^{3}}\) Hint: \(2^3 = 8\) is not a factor of 540. | |
\( \large{{2}^{2}}\cdot {{3}^{2}}\) Hint: This is a common factor of both numbers, but it's not the greatest common factor. |
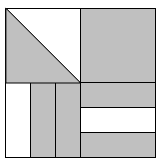
Question 5 |
Below are front, side, and top views of a three-dimensional solid.
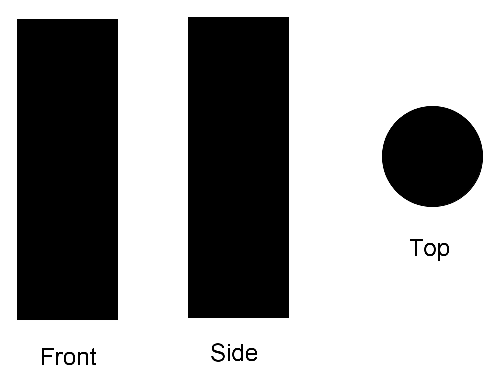
Which of the following could be the solid shown above?
A sphereHint: All views would be circles. | |
A cylinder | |
A coneHint: Two views would be triangles, not rectangles. | |
A pyramidHint: How would one view be a circle? |
Question 6 |
In which table below is y a function of x?
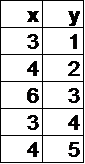 Hint: If x=3, y can have two different values, so it's not a function. | |
 Hint: If x=3, y can have two different values, so it's not a function. | |
 Hint: If x=1, y can have different values, so it's not a function. | |
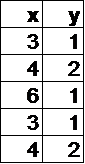 Hint: Each value of x always corresponds to the same value of y. |
Question 7 |
A biology class requires a lab fee, which is a whole number of dollars, and the same amount for all students. On Monday the instructor collected $70 in fees, on Tuesday she collected $126, and on Wednesday she collected $266. What is the largest possible amount the fee could be?
$2Hint: A possible fee, but not the largest possible fee. Check the other choices to see which are factors of all three numbers. | |
$7Hint: A possible fee, but not the largest possible fee. Check the other choices to see which are factors of all three numbers. | |
$14Hint: This is the greatest common factor of 70, 126, and 266. | |
$70Hint: Not a factor of 126 or 266, so couldn't be correct. |
Question 8 |
An above-ground swimming pool is in the shape of a regular hexagonal prism, is one meter high, and holds 65 cubic meters of water. A second pool has a base that is also a regular hexagon, but with sides twice as long as the sides in the first pool. This second pool is also one meter high. How much water will the second pool hold?
\( \large 65\text{ }{{\text{m}}^{3}}\) Hint: A bigger pool would hold more water. | |
\( \large 65\cdot 2\text{ }{{\text{m}}^{3}}\) Hint: Try a simpler example, say doubling the sides of the base of a 1 x 1 x 1 cube. | |
\( \large 65\cdot 4\text{ }{{\text{m}}^{3}}\) Hint: If we think of the pool as filled with 1 x 1 x 1 cubes (and some fractions of cubes), then scaling to the larger pool changes each 1 x 1 x 1 cube to a 2 x 2 x 1 prism, or multiplies volume by 4. | |
\( \large 65\cdot 8\text{ }{{\text{m}}^{3}}\) Hint: Try a simpler example, say doubling the sides of the base of a 1 x 1 x 1 cube. |
Question 9 |
The histogram below shows the frequency of a class's scores on a 4 question quiz.
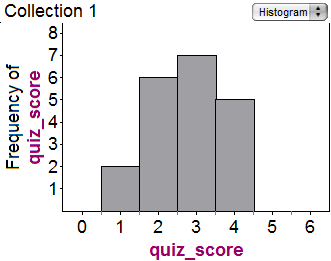
What was the mean score on the quiz?
\( \large 2.75\) Hint: There were 20 students who took the quiz. Total points earned: \(2 \times 1+6 \times 2+ 7\times 3+5 \times 4=55\), and 55/20 = 2.75. | |
\( \large 2\) Hint: How many students are there total? Did you count them all? | |
\( \large 3\) Hint: How many students are there total? Did you count them all? Be sure you're finding the mean, not the median or the mode. | |
\( \large 2.5\) Hint: How many students are there total? Did you count them all? Don't just take the mean of 1, 2, 3, 4 -- you have to weight them properly. |
Question 10 |
At a school fundraising event, people can buy a ticket to spin a spinner like the one below. The region that the spinner lands in tells which, if any, prize the person wins.

If 240 people buy tickets to spin the spinner, what is the best estimate of the number of keychains that will be given away?
40Hint: "Keychain" appears on the spinner twice. | |
80Hint: The probability of getting a keychain is 1/3, and so about 1/3 of the time the spinner will win. | |
100Hint: What is the probability of winning a keychain? | |
120Hint: That would be the answer for getting any prize, not a keychain specifically. |
Question 11 |
The prime factorization of n can be written as n=pqr, where p, q, and r are distinct prime numbers. How many factors does n have, including 1 and itself?
\( \large3\) Hint: 1, p, q, r, and pqr are already 5, so this isn't enough. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large5\) Hint: Don't forget pq, etc. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large6\) Hint: You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large8\) Hint: 1, p, q, r, pq, pr, qr, pqr. |
Question 12 |
\( \large \dfrac{17}{24}\) Hint: You might try adding segments so each quadrant is divided into 6 pieces with equal area -- there will be 24 regions, not all the same shape, but all the same area, with 17 of them shaded (for the top left quarter, you could also first change the diagonal line to a horizontal or vertical line that divides the square in two equal pieces and shade one) . | |
\( \large \dfrac{3}{4}\) Hint: Be sure you're taking into account the different sizes of the pieces. | |
\( \large \dfrac{2}{3}\) Hint: The bottom half of the picture is 2/3 shaded, and the top half is more than 2/3 shaded, so this answer is too small. | |
\( \large \dfrac{17}{6} \) Hint: This answer is bigger than 1, so doesn't make any sense. Be sure you are using the whole picture, not one quadrant, as the unit. |
Question 13 |
The picture below shows identical circles drawn on a piece of paper. The rectangle represents an index card that is blocking your view of \( \dfrac{3}{5}\) of the circles on the paper. How many circles are covered by the rectangle?

4Hint: The card blocks more than half of the circles, so this number is too small. | |
5Hint: The card blocks more than half of the circles, so this number is too small. | |
8Hint: The card blocks more than half of the circles, so this number is too small. | |
12Hint: 2/5 of the circles or 8 circles are showing. Thus 4 circles represent 1/5 of the circles, and \(4 \times 5=20\) circles represent 5/5 or all the circles. Thus 12 circles are hidden. |
Question 14 |
Which of the following is closest to the height of a college student in centimeters?
1.6 cmHint: This is more the height of a Lego toy college student -- less than an inch! | |
16 cmHint: Less than knee high on most college students. | |
160 cmHint: Remember, a meter stick (a little bigger than a yard stick) is 100 cm. Also good to know is that 4 inches is approximately 10 cm. | |
1600 cmHint: This college student might be taller than some campus buildings! |
Question 15 |
Which of the following is equivalent to
\( \large A-B+C\div D\times E\)?
\( \large A-B-\dfrac{C}{DE}
\) Hint: In the order of operations, multiplication and division have the same priority, so do them left to right; same with addition and subtraction. | |
\( \large A-B+\dfrac{CE}{D}\) Hint: In practice, you're better off using parentheses than writing an expression like the one in the question. The PEMDAS acronym that many people memorize is misleading. Multiplication and division have equal priority and are done left to right. They have higher priority than addition and subtraction. Addition and subtraction also have equal priority and are done left to right. | |
\( \large \dfrac{AE-BE+CE}{D}\) Hint: Use order of operations, don't just compute left to right. | |
\( \large A-B+\dfrac{C}{DE}\) Hint: In the order of operations, multiplication and division have the same priority, so do them left to right |
Question 16 |
Which of the lists below is in order from least to greatest value?
\( \large -0.044,\quad -0.04,\quad 0.04,\quad 0.044\) Hint: These are easier to compare if you add trailing zeroes (this is finding a common denominator) -- all in thousandths, -0.044, -0.040,0 .040, 0.044. The middle two numbers, -0.040 and 0.040 can be modeled as owing 4 cents and having 4 cents. The outer two numbers are owing or having a bit more. | |
\( \large -0.04,\quad -0.044,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. | |
\( \large -0.04,\quad -0.044,\quad 0.04,\quad 0.044\) Hint: -0.04=-0.040, which is greater than \(-0.044\). | |
\( \large -0.044,\quad -0.04,\quad 0.044,\quad 0.04\) Hint: 0.04=0.040, which is less than 0.044. |
Question 17 |
The histogram below shows the number of pairs of footware owned by a group of college students.
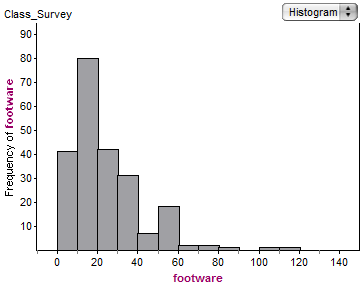
Which of the following statements can be inferred from the graph above?
The median number of pairs of footware owned is between 50 and 60 pairs.Hint: The same number of data points are less than the median as are greater than the median -- but on this histogram, clearly more than half the students own less than 50 pairs of shoes, so the median is less than 50. | |
The mode of the number of pairs of footware owned is 20.Hint: The mode is the most common number of pairs of footwear owned. We can't tell it from this histogram because each bar represents 10 different numbers-- perhaps 8 students each own each number from 10 to 19, but 40 students own exactly 6 pairs of shoes.... or perhaps not.... | |
The mean number of pairs of footware owned is less than the median number of pairs of footware owned.Hint: This is a right skewed distribution, and so the mean is bigger than the median -- the few large values on the right pull up the mean, but have little effect on the median. | |
The median number of pairs of footware owned is between 10 and 20.Hint: There are approximately 230 students represented in this survey, and the 41st through 120th lowest values are between 10 and 20 -- thus the middle value is in that range. |
Question 18 |
Below is a pictorial representation of \(2\dfrac{1}{2}\div \dfrac{2}{3}\):

Which of the following is the best description of how to find the quotient from the picture?
The quotient is \(3\dfrac{3}{4}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{4}\) of \(\dfrac{2}{3}\). | |
The quotient is \(3\dfrac{1}{2}\). There are 3 whole blocks each representing \(\dfrac{2}{3}\) and a partial block composed of 3 small rectangles. The 3 small rectangles represent \(\dfrac{3}{6}\) of a whole, or \(\dfrac{1}{2}\).Hint: We are counting how many 2/3's are in 2 1/2: the unit becomes 2/3, not 1. | |
The quotient is \(\dfrac{4}{15}\). There are four whole blocks separated into a total of 15 small rectangles.Hint: This explanation doesn't make much sense. Probably you are doing "invert and multiply," but inverting the wrong thing. | |
This picture cannot be used to find the quotient because it does not show how to separate \(2\dfrac{1}{2}\) into equal sized groups.Hint: Study the measurement/quotative model of division. It's often very useful with fractions. |
Question 19 |
Use the four figures below to answer the question that follows:

How many of the figures pictured above have at least one line of reflective symmetry?
\( \large 1\) | |
\( \large 2\) Hint: The ellipse has 2 lines of reflective symmetry (horizontal and vertical, through the center) and the triangle has 3. The other two figures have rotational symmetry, but not reflective symmetry. | |
\( \large 3\) | |
\( \large 4\) Hint: All four have rotational symmetry, but not reflective symmetry. |
Question 20 |
Which of the following nets will not fold into a cube?
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
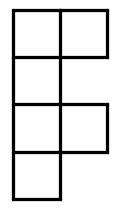 | |
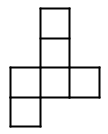 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). | |
 Hint: If you have trouble visualizing, cut them out and fold (during the test, you can tear paper to approximate). |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.