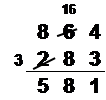Hints will display for most wrong answers; explanations for most right answers. You can attempt a question multiple times; it will only be scored correct if you get it right the first time.
I used the official objectives and sample test to construct these questions, but cannot promise that they accurately reflect what’s on the real test. Some of the sample questions were more convoluted than I could bear to write. See terms of use. See the MTEL Practice Test main page to view questions on a particular topic or to download paper practice tests.
MTEL General Curriculum Mathematics Practice
Question 1 |
The window glass below has the shape of a semi-circle on top of a square, where the side of the square has length x. It was cut from one piece of glass.
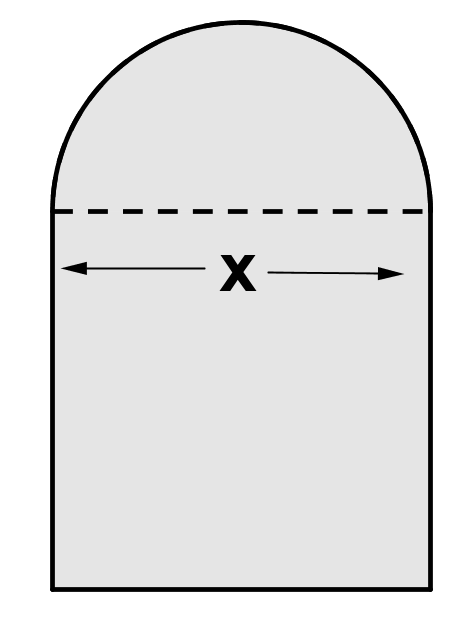
What is the perimeter of the window glass?
\( \large 3x+\dfrac{\pi x}{2}\) Hint: By definition, \(\pi\) is the ratio of the circumference of a circle to its diameter; thus the circumference is \(\pi d\). Since we have a semi-circle, its perimeter is \( \dfrac{1}{2} \pi x\). Only 3 sides of the square contribute to the perimeter. | |
\( \large 3x+2\pi x\) Hint: Make sure you know how to find the circumference of a circle. | |
\( \large 3x+\pi x\) Hint: Remember it's a semi-circle, not a circle. | |
\( \large 4x+2\pi x\) Hint: Only 3 sides of the square contribute to the perimeter. |
Question 2 |
Some children explored the diagonals in 2 x 2 squares on pages of a calendar (where all four squares have numbers in them). They conjectured that the sum of the diagonals is always equal; in the example below, 8+16=9+15.
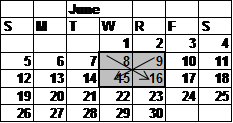
Which of the equations below could best be used to explain why the children's conjecture is correct?
\( \large 8x+16x=9x+15x\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. | |
\( \large x+(x+2)=(x+1)+(x+1)\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. | |
\( \large x+(x+8)=(x+1)+(x+7)\) Hint: x is the number in the top left square, x+8 is one below and to the right, x+1 is to the right of x, and x+7 is below x. | |
\( \large x+8+16=x+9+15\) Hint: What would x represent in this case? Make sure you can describe in words what x represents. |
Question 3 |
A family on vacation drove the first 200 miles in 4 hours and the second 200 miles in 5 hours. Which expression below gives their average speed for the entire trip?
\( \large \dfrac{200+200}{4+5}\) Hint: Average speed is total distance divided by total time. | |
\( \large \left( \dfrac{200}{4}+\dfrac{200}{5} \right)\div 2\) Hint: This seems logical, but the problem is that it weights the first 4 hours and the second 5 hours equally, when each hour should get the same weight in computing the average speed. | |
\( \large \dfrac{200}{4}+\dfrac{200}{5} \) Hint: This would be an average of 90 miles per hour! | |
\( \large \dfrac{400}{4}+\dfrac{400}{5} \) Hint: This would be an average of 180 miles per hour! Even a family of race car drivers probably doesn't have that average speed on a vacation! |
Question 4 |
| I. \(\large \dfrac{1}{2}+\dfrac{1}{3}\) | II. \( \large .400000\) | III. \(\large\dfrac{1}{5}+\dfrac{1}{5}\) |
| IV. \( \large 40\% \) | V. \( \large 0.25 \) | VI. \(\large\dfrac{14}{35}\) |
Which of the lists below includes all of the above expressions that are equivalent to \( \dfrac{2}{5}\)?
I, III, V, VIHint: I and V are not at all how fractions and decimals work. | |
III, VIHint: These are right, but there are more. | |
II, III, VIHint: These are right, but there are more. | |
II, III, IV, VI |
Question 5 |
Use the expression below to answer the question that follows.
\(\large \dfrac{\left( 155 \right)\times \left( 6,124 \right)}{977}\)
Which of the following is the best estimate of the expression above?
100Hint: 6124/977 is approximately 6. | |
200Hint: 6124/977 is approximately 6. | |
1,000Hint: 6124/977 is approximately 6. 155 is approximately 150, and \( 6 \times 150 = 3 \times 300 = 900\), so this answer is closest. | |
2,000Hint: 6124/977 is approximately 6. |
Question 6 |
The pattern below consists of a row of black squares surrounded by white squares.
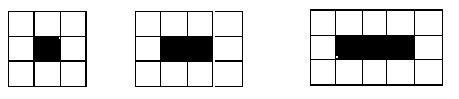
How many white squares would surround a row of 157 black squares?
314Hint: Try your procedure on a smaller number that you can count to see where you made a mistake. | |
317Hint: Are there ever an odd number of white squares? | |
320Hint: One way to see this is that there are 6 tiles on the left and right ends, and the rest of the white tiles are twice the number of black tiles (there are many other ways to look at it too). | |
322Hint: Try your procedure on a smaller number that you can count to see where you made a mistake. |
Question 7 |
Cell phone plan A charges $3 per month plus $0.10 per minute. Cell phone plan B charges $29.99 per month, with no fee for the first 400 minutes and then $0.20 for each additional minute.
Which equation can be used to solve for the number of minutes, m (with m>400) that a person would have to spend on the phone each month in order for the bills for plan A and plan B to be equal?
\( \large 3.10m=400+0.2m\) Hint: These are the numbers in the problem, but this equation doesn't make sense. If you don't know how to make an equation, try plugging in an easy number like m=500 minutes to see if each side equals what it should. | |
\( \large 3+0.1m=29.99+.20m\) Hint: Doesn't account for the 400 free minutes. | |
\( \large 3+0.1m=400+29.99+.20(m-400)\) Hint: Why would you add 400 minutes and $29.99? If you don't know how to make an equation, try plugging in an easy number like m=500 minutes to see if each side equals what it should. | |
\( \large 3+0.1m=29.99+.20(m-400)\) Hint: The left side is $3 plus $0.10 times the number of minutes. The right is $29.99 plus $0.20 times the number of minutes over 400. |
Question 8 |
The Venn Diagram below gives data on the number of seniors, athletes, and vegetarians in the student body at a college:
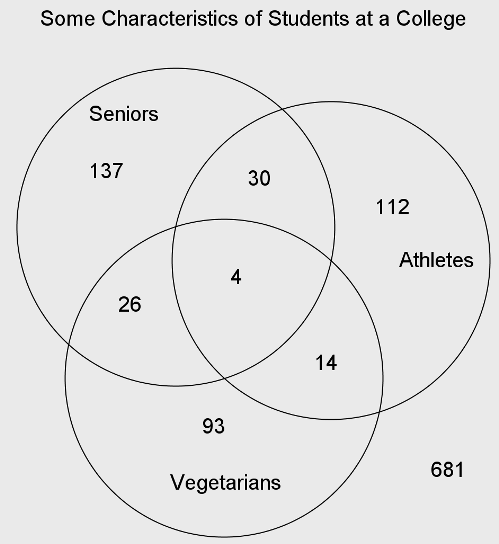
How many students at the college are seniors who are not vegetarians?
\( \large 137\) Hint: Doesn't include the senior athletes who are not vegetarians. | |
\( \large 167\) | |
\( \large 197\) Hint: That's all seniors, including vegetarians. | |
\( \large 279\) Hint: Includes all athletes who are not vegetarians, some of whom are not seniors. |
Question 9 |
The following story situations model \( 12\div 3\):
I) Jack has 12 cookies, which he wants to share equally between himself and two friends. How many cookies does each person get?
II) Trent has 12 cookies, which he wants to put into bags of 3 cookies each. How many bags can he make?
III) Cicely has $12. Cookies cost $3 each. How many cookies can she buy?
Which of these questions illustrate the same model of division, either partitive (partioning) or measurement (quotative)?
I and II | |
I and III | |
II and IIIHint: Problem I is partitive (or partitioning or sharing) -- we put 12 objects into 3 groups. Problems II and III are quotative (or measurement) -- we put 12 objects in groups of 3. | |
All three problems model the same meaning of division |
Question 10 |
Use the graph below to answer the question that follows.

Which of the following is a correct equation for the graph of the line depicted above?
\( \large y=-\dfrac{1}{2}x+2\) Hint: The slope is -1/2 and the y-intercept is 2. You can also try just plugging in points. For example, this is the only choice that gives y=1 when x=2. | |
\( \large 4x=2y\) Hint: This line goes through (0,0); the graph above does not. | |
\( \large y=x+2\) Hint: The line pictured has negative slope. | |
\( \large y=-x+2\) Hint: Try plugging x=4 into this equation and see if that point is on the graph above. |
Question 11 |
The prime factorization of n can be written as n=pqr, where p, q, and r are distinct prime numbers. How many factors does n have, including 1 and itself?
\( \large3\) Hint: 1, p, q, r, and pqr are already 5, so this isn't enough. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large5\) Hint: Don't forget pq, etc. You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large6\) Hint: You might try plugging in p=2, q=3, and r=5 to help with this problem. | |
\( \large8\) Hint: 1, p, q, r, pq, pr, qr, pqr. |
Question 12 |
In each expression below N represents a negative integer. Which expression could have a negative value?
\( \large {{N}^{2}}\) Hint: Squaring always gives a non-negative value. | |
\( \large 6-N\) Hint: A story problem for this expression is, if it was 6 degrees out at noon and N degrees out at sunrise, by how many degrees did the temperature rise by noon? Since N is negative, the answer to this question has to be positive, and more than 6. | |
\( \large -N\) Hint: If N is negative, then -N is positive | |
\( \large 6+N\) Hint: For example, if \(N=-10\), then \(6+N = -4\) |
Question 13 |
The column below consists of two cubes and a cylinder. The cylinder has diameter y, which is also the length of the sides of each cube. The total height of the column is 5y. Which of the formulas below gives the volume of the column?

\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{4}\) Hint: The cubes each have volume \(y^3\). The cylinder has radius \(\dfrac{y}{2}\) and height \(3y\). The volume of a cylinder is \(\pi r^2 h=\pi ({\dfrac{y}{2}})^2(3y)=\dfrac{3\pi {{y}^{3}}}{4}\). Note that the volume of a cylinder is analogous to that of a prism -- area of the base times height. | |
\( \large 2{{y}^{3}}+3\pi {{y}^{3}}\) Hint: y is the diameter of the circle, not the radius. | |
\( \large {{y}^{3}}+5\pi {{y}^{3}}\) Hint: Don't forget to count both cubes. | |
\( \large 2{{y}^{3}}+\dfrac{3\pi {{y}^{3}}}{8}\) Hint: Make sure you know how to find the volume of a cylinder. |
Question 14 |
The "houses" below are made of toothpicks and gum drops.
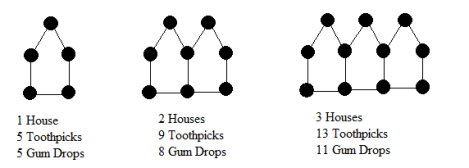
Which of the following does not represent the number of gumdrops in a row of h houses?
\( \large 2+3h\) Hint: Think of this as start with 2 gumdrops on the left wall, and then add 3 gumdrops for each house. | |
\( \large 5+3(h-1)\) Hint: Think of this as start with one house, and then add 3 gumdrops for each of the other h-1 houses. | |
\( \large h+(h+1)+(h+1)\) Hint: Look at the gumdrops in 3 rows: h gumdrops for the "rooftops," h+1 for the tops of the vertical walls, and h+1 for the floors. | |
\( \large 5+3h\) Hint: This one is not a correct equation (which makes it the correct answer!). Compare to choice A. One of them has to be wrong, as they differ by 3. |
Question 15 |
Which of the following is an irrational number?
\( \large \sqrt[3]{8}\) Hint: This answer is the cube root of 8. Since 2 x 2 x 2 =8, this is equal to 2, which is rational because 2 = 2/1. | |
\( \large \sqrt{8}\) Hint: It is not trivial to prove that this is irrational, but you can get this answer by eliminating the other choices. | |
\( \large \dfrac{1}{8}\) Hint: 1/8 is the RATIO of two integers, so it is rational. | |
\( \large -8\) Hint: Negative integers are also rational, -8 = -8/1, a ratio of integers. |
Question 16 |
Which of the lists below contains only irrational numbers?
\( \large\pi , \quad \sqrt{6},\quad \sqrt{\dfrac{1}{2}}\) | |
\( \large\pi , \quad \sqrt{9}, \quad \pi +1\) Hint: \( \sqrt{9}=3\) | |
\( \large\dfrac{1}{3},\quad \dfrac{5}{4},\quad \dfrac{2}{9}\) Hint: These are all rational. | |
\( \large-3,\quad 14,\quad 0\) Hint: These are all rational. |
Question 17 |
Use the graph below to answer the question that follows:
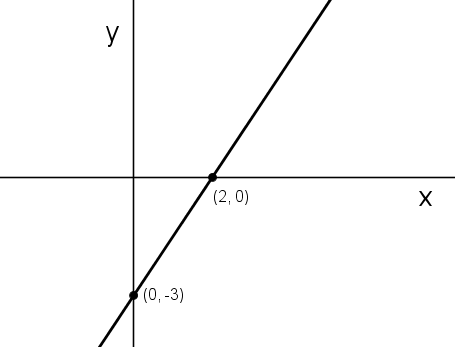
The graph above represents the equation \( \large 3x+Ay=B\), where A and B are integers. What are the values of A and B?
\( \large A = -2, B= 6\) Hint: Plug in (2,0) to get B=6, then plug in (0,-3) to get A=-2. | |
\( \large A = 2, B = 6\) Hint: Try plugging (0,-3) into this equation. | |
\( \large A = -1.5, B=-3\) Hint: The problem said that A and B were integers and -1.5 is not an integer. Don't try to use slope-intercept form. | |
\( \large A = 2, B = -3\) Hint: Try plugging (2,0) into this equation. |
Question 18 |
Elena is going to use a calculator to check whether or not 267 is prime. She will pick certain divisors, and then find 267 divided by each, and see if she gets a whole number. If she never gets a whole number, then she's found a prime. Which numbers does Elena NEED to check before she can stop checking and be sure she has a prime?
All natural numbers from 2 to 266.Hint: She only needs to check primes -- checking the prime factors of any composite is enough to look for divisors. As a test taking strategy, the other three choices involve primes, so worth thinking about. | |
All primes from 2 to 266 .Hint: Remember, factors come in pairs (except for square root factors), so she would first find the smaller of the pair and wouldn't need to check the larger. | |
All primes from 2 to 133 .Hint: She doesn't need to check this high. Factors come in pairs, and something over 100 is going to be paired with something less than 3, so she will find that earlier. | |
All primes from \( \large 2\) to \( \large \sqrt{267}\).Hint: \(\sqrt{267} \times \sqrt{267}=267\). Any other pair of factors will have one factor less than \( \sqrt{267}\) and one greater, so she only needs to check up to \( \sqrt{267}\). |
Question 19 |
A homeowner is planning to tile the kitchen floor with tiles that measure 6 inches by 8 inches. The kitchen floor is a rectangle that measures 10 ft by 12 ft, and there are no gaps between the tiles. How many tiles does the homeowner need?
30Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. Also, remember that 1 sq foot is 12 \(\times\) 12=144 sq inches. | |
120Hint: The floor is 120 sq feet, and the tiles are smaller than 1 sq foot. | |
300Hint: Recheck your calculations. | |
360Hint: One way to do this is to note that 6 inches = 1/2 foot and 8 inches = 2/3 foot, so the area of each tile is 1/2 \(\times\) 2/3=1/3 sq foot, or each square foot of floor requires 3 tiles. The area of the floor is 120 square feet. Note that the tiles would fit evenly oriented in either direction, parallel to the walls. |
Question 20 |
In the triangle below, \(\overline{AC}\cong \overline{AD}\cong \overline{DE}\) and \(m\angle CAD=100{}^\circ \). What is \(m\angle DAE\)?
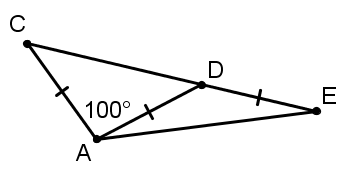
\( \large 20{}^\circ \) Hint: Angles ACD and ADC are congruent since they are base angles of an isosceles triangle. Since the angles of a triangle sum to 180, they sum to 80, and they are 40 deg each. Thus angle ADE is 140 deg, since it makes a straight line with angle ADC. Angles DAE and DEA are base angles of an isosceles triangle and thus congruent-- they sum to 40 deg, so are 20 deg each. | |
\( \large 25{}^\circ \) Hint: If two sides of a triangle are congruent, then it's isosceles, and the base angles of an isosceles triangle are equal. | |
\( \large 30{}^\circ \) Hint: If two sides of a triangle are congruent, then it's isosceles, and the base angles of an isosceles triangle are equal. | |
\( \large 40{}^\circ \) Hint: Make sure you're calculating the correct angle. |
Question 21 |
Below is a portion of a number line:

Point B is halfway between two tick marks. What number is represented by Point B?
\( \large 0.645\) Hint: That point is marked on the line, to the right. | |
\( \large 0.6421\) Hint: That point is to the left of point B. | |
\( \large 0.6422\) Hint: That point is to the left of point B. | |
\( \large 0.6425\) |
Question 22 |
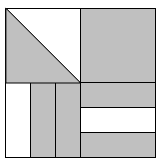
\( \large \dfrac{17}{24}\) Hint: You might try adding segments so each quadrant is divided into 6 pieces with equal area -- there will be 24 regions, not all the same shape, but all the same area, with 17 of them shaded (for the top left quarter, you could also first change the diagonal line to a horizontal or vertical line that divides the square in two equal pieces and shade one) . | |
\( \large \dfrac{3}{4}\) Hint: Be sure you're taking into account the different sizes of the pieces. | |
\( \large \dfrac{2}{3}\) Hint: The bottom half of the picture is 2/3 shaded, and the top half is more than 2/3 shaded, so this answer is too small. | |
\( \large \dfrac{17}{6} \) Hint: This answer is bigger than 1, so doesn't make any sense. Be sure you are using the whole picture, not one quadrant, as the unit. |
Question 23 |
The function d(x) gives the result when 12 is divided by x. Which of the following is a graph of d(x)?
 Hint: d(x) is 12 divided by x, not x divided by 12. | |
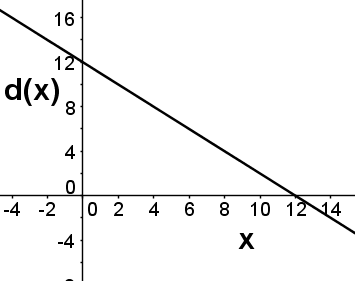 Hint: When x=2, what should d(x) be? | |
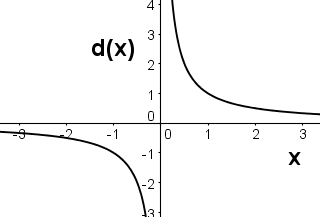 Hint: When x=2, what should d(x) be? | |
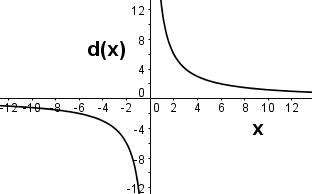 |
Question 24 |
P is a prime number that divides 240. Which of the following must be true?
P divides 30Hint: 2, 3, and 5 are the prime factors of 240, and all divide 30. | |
P divides 48Hint: P=5 doesn't work. | |
P divides 75Hint: P=2 doesn't work. | |
P divides 80Hint: P=3 doesn't work. |
Question 25 |
Here is a student's work solving an equation:
\( x-4=-2x+6\)
\( x-4+4=-2x+6+4\)
\( x=-2x+10\)
\( x-2x=10\)
\( x=10\)
Which of the following statements is true?
The student‘s solution is correct.Hint: Try plugging into the original solution. | |
The student did not correctly use properties of equality.Hint: After \( x=-2x+10\), the student subtracted 2x on the left and added 2x on the right. | |
The student did not correctly use the distributive property.Hint: Distributive property is \(a(b+c)=ab+ac\). | |
The student did not correctly use the commutative property.Hint: Commutative property is \(a+b=b+a\) or \(ab=ba\). |
Question 26 |
A solution requires 4 ml of saline for every 7 ml of medicine. How much saline would be required for 50 ml of medicine?
\( \large 28 \dfrac{4}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. The extra ml of saline requires 4 ml saline/ 7 ml medicine = 4/7 ml saline per 1 ml medicine. | |
\( \large 28 \dfrac{1}{4}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 28 \dfrac{1}{7}\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? | |
\( \large 87.5\) ml Hint: 49 ml of medicine requires 28 ml of saline. How much saline does the extra ml require? |
Question 27 |
Aya and Kendra want to estimate the height of a tree. On a sunny day, Aya measures Kendra's shadow as 3 meters long, and Kendra measures the tree's shadow as 15 meters long. Kendra is 1.5 meters tall. How tall is the tree?
7.5 metersHint: Here is a picture, note that the large and small right triangles are similar:  One way to do the problem is to note that there is a dilation (scale) factor of 5 on the shadows, so there must be that factor on the heights too. Another way is to note that the shadows are twice as long as the heights. | |
22.5 metersHint: Draw a picture. | |
30 metersHint: Draw a picture. | |
45 metersHint: Draw a picture. |
Question 28 |
Use the samples of a student's work below to answer the question that follows:
This student divides fractions by first finding a common denominator, then dividing the numerators.
\( \large \dfrac{2}{3} \div \dfrac{3}{4} \longrightarrow \dfrac{8}{12} \div \dfrac{9}{12} \longrightarrow 8 \div 9 = \dfrac {8}{9}\) \( \large \dfrac{2}{5} \div \dfrac{7}{20} \longrightarrow \dfrac{8}{20} \div \dfrac{7}{20} \longrightarrow 8 \div 7 = \dfrac {8}{7}\) \( \large \dfrac{7}{6} \div \dfrac{3}{4} \longrightarrow \dfrac{14}{12} \div \dfrac{9}{12} \longrightarrow 14 \div 9 = \dfrac {14}{9}\)Which of the following best describes the mathematical validity of the algorithm the student is using?
It is not valid. Common denominators are for adding and subtracting fractions, not for dividing them.Hint: Don't be so rigid! Usually there's more than one way to do something in math. | |
It got the right answer in these three cases, but it isn‘t valid for all rational numbers.Hint: Did you try some other examples? What makes you say it's not valid? | |
It is valid if the rational numbers in the division problem are in lowest terms and the divisor is not zero.Hint: Lowest terms doesn't affect this problem at all. | |
It is valid for all rational numbers, as long as the divisor is not zero.Hint: When we have common denominators, the problem is in the form a/b divided by c/b, and the answer is a/c, as the student's algorithm predicts. |
Question 29 |
The student used a method that worked for this problem and can be generalized to any subtraction problem.Hint: Note that this algorithm is taught as the "standard" algorithm in much of Europe (it's where the term "borrowing" came from -- you borrow on top and "pay back" on the bottom). | |
The student used a method that worked for this problem and that will work for any subtraction problem that only requires one regrouping; it will not work if more regrouping is required.Hint: Try some more examples. | |
The student used a method that worked for this problem and will work for all three-digit subtraction problems, but will not work for larger problems.Hint: Try some more examples. | |
The student used a method that does not work. The student made two mistakes that cancelled each other out and was lucky to get the right answer for this problem.Hint: Remember, there are many ways to do subtraction; there is no one "right" algorithm. |
Question 30 |
The least common multiple of 60 and N is 1260. Which of the following could be the prime factorization of N?
\( \large2\cdot 5\cdot 7\) Hint: 1260 is divisible by 9 and 60 is not, so N must be divisible by 9 for 1260 to be the LCM. | |
\( \large{{2}^{3}}\cdot {{3}^{2}}\cdot 5 \cdot 7\) Hint: 1260 is not divisible by 8, so it isn't a multiple of this N. | |
\( \large3 \cdot 5 \cdot 7\) Hint: 1260 is divisible by 9 and 60 is not, so N must be divisible by 9 for 1260 to be the LCM. | |
\( \large{{3}^{2}}\cdot 5\cdot 7\) Hint: \(1260=2^2 \cdot 3^2 \cdot 5 \cdot 7\) and \(60=2^2 \cdot 3 \cdot 5\). In order for 1260 to be the LCM, N has to be a multiple of \(3^2\) and of 7 (because 60 is not a multiple of either of these). N also cannot introduce a factor that would require the LCM to be larger (as in choice b). |
Question 31 |
Use the table below to answer the question that follows:
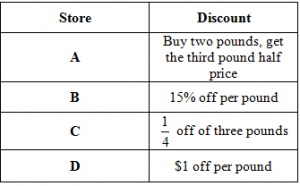
Gordon wants to buy three pounds of nuts. Each of the stores above ordinarily sells the nuts for $4.99 a pound, but is offering a discount this week. At which store can he buy the nuts for the least amount of money?
Store AHint: This would save about $2.50. You can quickly see that D saves more. | |
Store BHint: This saves 15% and C saves 25%. | |
Store C | |
Store DHint: This is about 20% off, which is less of a discount than C. |
Question 32 |
How many lines of reflective symmetry and how many centers of rotational symmetry does the parallelogram depicted below have?

4 lines of reflective symmetry, 1 center of rotational symmetry.Hint: Try cutting out a shape like this one from paper, and fold where you think the lines of reflective symmetry are (or put a mirror there). Do things line up as you thought they would? | |
2 lines of reflective symmetry, 1 center of rotational symmetry.Hint: Try cutting out a shape like this one from paper, and fold where you think the lines of reflective symmetry are (or put a mirror there). Do things line up as you thought they would? | |
0 lines of reflective symmetry, 1 center of rotational symmetry.Hint: The intersection of the diagonals is a center of rotational symmetry. There are no lines of reflective symmetry, although many people get confused about this fact (best to play with hands on examples to get a feel). Just fyi, the letter S also has rotational, but not reflective symmetry, and it's one that kids often write backwards. | |
2 lines of reflective symmetry, 0 centers of rotational symmetry.Hint: Try cutting out a shape like this one from paper. Trace onto another sheet of paper. See if there's a way to rotate the cut out shape (less than a complete turn) so that it fits within the outlines again. |
Question 33 |
Here are some statements:
I) 5 is an integer II)\( -5 \) is an integer III) \(0\) is an integer
Which of the statements are true?
I only | |
I and II only | |
I and III only | |
I, II, and IIIHint: The integers are ...-3, -2, -1, 0, 1, 2, 3, .... |
Question 34 |
The equation \( \large F=\frac{9}{5}C+32\) is used to convert a temperature measured in Celsius to the equivalent Farentheit temperature.
A patient's temperature increased by 1.5° Celcius. By how many degrees Fahrenheit did her temperature increase?
1.5°Hint: Celsius and Fahrenheit don't increase at the same rate. | |
1.8°Hint: That's how much the Fahrenheit temp increases when the Celsius temp goes up by 1 degree. | |
2.7°Hint: Each degree increase in Celsius corresponds to a \(\dfrac{9}{5}=1.8\) degree increase in Fahrenheit. Thus the increase is 1.8+0.9=2.7. | |
Not enough information.Hint: A linear equation has constant slope, which means that every increase of the same amount in one variable, gives a constant increase in the other variable. It doesn't matter what temperature the patient started out at. |
Question 35 |
The "houses" below are made of toothpicks and gum drops.

How many toothpicks are there in a row of 53 houses?
212Hint: Can the number of toothpicks be even? | |
213Hint: One way to see this is that every new "house" adds 4 toothpicks to the leftmost vertical toothpick -- so the total number is 1 plus 4 times the number of "houses." There are many other ways to look at the problem too. | |
217Hint: Try your strategy with a smaller number of "houses" so you can count and find your mistake. | |
265Hint: Remember that the "houses" overlap some walls. |
Question 36 |
Which of the following sets of polygons can be assembled to form a pentagonal pyramid?
2 pentagons and 5 rectangles.Hint: These can be assembled to form a pentagonal prism, not a pentagonal pyramid. | |
1 square and 5 equilateral triangles.Hint: You need a pentagon for a pentagonal pyramid. | |
1 pentagon and 5 isosceles triangles. | |
1 pentagon and 10 isosceles triangles. |
Question 37 |
If x is an integer, which of the following must also be an integer?
\( \large \dfrac{x}{2}\) Hint: If x is odd, then \( \dfrac{x}{2} \) is not an integer, e.g. 3/2 = 1.5. | |
\( \large \dfrac{2}{x}\) Hint: Only an integer if x = -2, -1, 1, or 2. | |
\( \large-x\) Hint: -1 times any integer is still an integer. | |
\(\large\sqrt{x}\) Hint: Usually not an integer, e.g. \( \sqrt{2} \approx 1.414 \). |
Question 38 |
Which of the lists below is in order from least to greatest value?
\( \large \dfrac{1}{2},\quad \dfrac{1}{3},\quad \dfrac{1}{4},\quad \dfrac{1}{5}\) Hint: This is ordered from greatest to least. | |
\( \large \dfrac{1}{3},\quad \dfrac{2}{7},\quad \dfrac{3}{8},\quad \dfrac{4}{11}\) Hint: 1/3 = 2/6 is bigger than 2/7. | |
\( \large \dfrac{1}{4},\quad \dfrac{2}{5},\quad \dfrac{2}{3},\quad \dfrac{4}{5}\) Hint: One way to look at this: 1/4 and 2/5 are both less than 1/2, and 2/3 and 4/5 are both greater than 1/2. 1/4 is 25% and 2/5 is 40%, so 2/5 is greater. The distance from 2/3 to 1 is 1/3 and from 4/5 to 1 is 1/5, and 1/5 is less than 1/3, so 4/5 is bigger. | |
\( \large \dfrac{7}{8},\quad \dfrac{6}{7},\quad \dfrac{5}{6},\quad \dfrac{4}{5}\) Hint: This is in order from greatest to least. |
Question 39 |
What is the mathematical name of the three-dimensional polyhedron depicted below?

TetrahedronHint: All the faces of a tetrahedron are triangles. | |
Triangular PrismHint: A prism has two congruent, parallel bases, connected by parallelograms (since this is a right prism, the parallelograms are rectangles). | |
Triangular PyramidHint: A pyramid has one base, not two. | |
TrigonHint: A trigon is a triangle (this is not a common term). |
Question 40 |
Here is a number trick:
1) Pick a whole number
2) Double your number.
3) Add 20 to the above result.
4) Multiply the above by 5
5) Subtract 100
6) Divide by 10
The result is always the number that you started with! Suppose you start by picking N. Which of the equations below best demonstrates that the result after Step 6 is also N?
\( \large N*2+20*5-100\div 10=N\) Hint: Use parentheses or else order of operations is off. | |
\( \large \left( \left( 2*N+20 \right)*5-100 \right)\div 10=N\) | |
\( \large \left( N+N+20 \right)*5-100\div 10=N\) Hint: With this answer you would subtract 10, instead of subtracting 100 and then dividing by 10. | |
\( \large \left( \left( \left( N\div 10 \right)-100 \right)*5+20 \right)*2=N\) Hint: This answer is quite backwards. |
Question 41 |
Use the problem below to answer the question that follows:
T shirts are on sale for 20% off. Tasha paid $8.73 for a shirt. What is the regular price of the shirt? There is no tax on clothing purchases under $175.
Let p represent the regular price of these t-shirt. Which of the following equations is correct?
\( \large 0.8p=\$8.73\) Hint: 80% of the regular price = $8.73. | |
\( \large \$8.73+0.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice c. | |
\( \large 1.2*\$8.73=p\) Hint: The 20% off was off of the ORIGINAL price, not off the $8.73 (a lot of people make this mistake). Plus this is the same equation as in choice b. | |
\( \large p-0.2*\$8.73=p\) Hint: Subtract p from both sides of this equation, and you have -.2 x 8.73 =0. |
Question 42 |
If two fair coins are flipped, what is the probability that one will come up heads and the other tails?
\( \large \dfrac{1}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{3} \) Hint: This is a very common misconception. There are three possible outcomes -- both heads, both tails, and one of each -- but they are not equally likely. Think of the coins as a penny and a dime, and list all possibilities. | |
\( \large \dfrac{1}{2}\) Hint: The possibilities are HH, HT, TH, TT, and all are equally likely. Two of the four have one of each coin, so the probability is 2/4=1/2. | |
\( \large \dfrac{3}{4}\) Hint: Think of the coins as a penny and a dime, and list all possibilities. |
Question 43 |
What set of transformations will transform the leftmost image into the rightmost image?
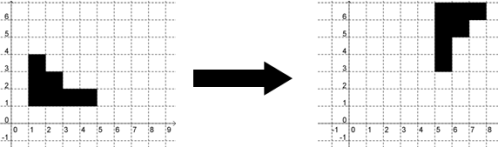
A 90 degree clockwise rotation about (2,1) followed by a translation of two units to the right.Hint: Part of the figure would move below the x-axis with these transformations. | |
A translation 3 units up, followed by a reflection about the line y=x.Hint: See what happens to the point (5,1) under this set of transformations. | |
A 90 degree clockwise rotation about (5,1), followed by a translation of 2 units up. | |
A 90 degree clockwise rotation about (2,1) followed by a translation of 2 units to the right.Hint: See what happens to the point (3,3) under this set of transformations. |
Question 44 |
There are 15 students for every teacher. Let t represent the number of teachers and let s represent the number of students. Which of the following equations is correct?
\( \large t=s+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large s=t+15\) Hint: When there are 2 teachers, how many students should there be? Do those values satisfy this equation? | |
\( \large t=15s\) Hint: This is a really easy mistake to make, which comes from transcribing directly from English, "1 teachers equals 15 students." To see that it's wrong, plug in s=2; do you really need 30 teachers for 2 students? To avoid this mistake, insert the word "number," "Number of teachers equals 15 times number of students" is more clearly problematic. | |
\( \large s=15t\) |
Question 45 |
The table below gives data from various years on how many young girls drank milk.

Based on the data given above, what was the probability that a randomly chosen girl in 1990 drank milk?
\( \large \dfrac{502}{1222}\) Hint: This is the probability that a randomly chosen girl who drinks milk was in the 1989-1991 food survey. | |
\( \large \dfrac{502}{2149}\) Hint: This is the probability that a randomly chosen girl from the whole survey drank milk and was also surveyed in 1989-1991. | |
\( \large \dfrac{502}{837}\) | |
\( \large \dfrac{1222}{2149}\) Hint: This is the probability that a randomly chosen girl from any year of the survey drank milk. |
|
List |
If you found a mistake or have comments on a particular question, please contact me (please copy and paste at least part of the question into the form, as the numbers change depending on how quizzes are displayed). General comments can be left here.